
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于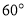 ;
;
(2)已知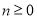 ,试用分析法证明:
,试用分析法证明: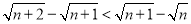 .
.
(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)根据应用反证法证明命题的一般步骤,先假设原命题的结论不成立,由此找出矛盾(本题中的矛盾指向:三角形的内角和定理),从而肯定结论进行证明即可;(2)根据分析法的思路是执果索因,要证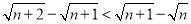 ,只需证
,只需证 ,进而结合不等式的性质:不等式的可乘方性,进行逐渐整理即可得到最后只须证
,进而结合不等式的性质:不等式的可乘方性,进行逐渐整理即可得到最后只须证 ,显然
,显然 成立,从而命题得证.
成立,从而命题得证.
试题解析:(1)证明:假设在一个三角形中,没有一个内角大于或等于 ,即均小于
,即均小于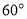
则三内角和小于 ,与三角形中三内角和等于
,与三角形中三内角和等于 矛盾,故假设不成立,原命题成立;
矛盾,故假设不成立,原命题成立;
(2)证明:要证上式成立,需证
需证
需证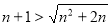
需证
需证
只需证
因为 显然成立,所以原命题成立.
显然成立,所以原命题成立.
考点:1.反证法;2.分析法.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科数学试卷(A)(解析版) 题型:选择题
设某大学的女生体重 (单位:
(单位: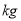 )与身高
)与身高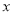 (单位:
(单位: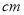 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据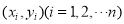 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为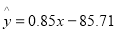 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.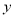 与
与 具有正的线性相关关系
具有正的线性相关关系
B.回归直线过样本点的中心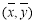
C.若该大学某女生身高增加lcm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试文科数学试卷(A)(解析版) 题型:选择题
已知抛物线关于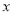 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点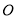 ,并且经过点
,并且经过点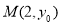 ,若点
,若点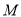 到该抛物线焦点的距离为3,则
到该抛物线焦点的距离为3,则 =( )
=( )
A.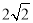 B.
B. C.4 D.
C.4 D.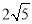
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
在线性回归模型 中,下列说法正确的是( )
中,下列说法正确的是( )
A. 是一次函数
是一次函数
B.因变量 是由自变量
是由自变量 唯一确定的
唯一确定的
C.因变量 除了受自变量
除了受自变量 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差
的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的产生
的产生
D.随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差
是由于计算不准确造成的,可以通过精确计算避免随机误差 的产生
的产生
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二普通班上学期期中理科数学试卷(解析版) 题型:选择题
下列结论正确的是( )
A.当x>0且x≠1时,
B.当x>0时,
C.当x≥2时,
D.当0<x≤2时, 无最大值
无最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com