
���� ��1���������b=1��e=$\frac{\sqrt{3}}{2}$=$\frac{c}{a}$���Ӷ�����ԲM�ķ��̼��ɣ�
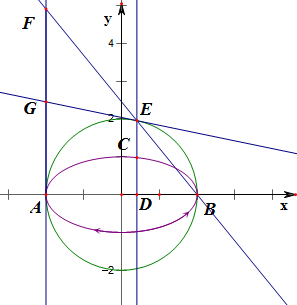
��2����������������ͼ����C��2cos�ȣ�sin�ȣ���F��-2��y�����Ӷ��ɵ�E��2cos�ȣ�2sin�ȣ�����F��-2��4$\frac{sin��}{1-cos��}$����G��-2��2$\frac{sin��}{1-cos��}$�����Ӷ��ɵ�$\overrightarrow{EG}$=��-2-2cos�ȣ�2$\frac{sin��}{1-cos��}$-2sin�ȣ���$\overrightarrow{OE}$=��2cos�ȣ�2sin�ȣ����Ӷ�֤��ֱ��GE����ABΪֱ����Բ�����ߣ�
���  �⣺��1��������ã�b=1��e=$\frac{\sqrt{3}}{2}$=$\frac{c}{a}$��
�⣺��1��������ã�b=1��e=$\frac{\sqrt{3}}{2}$=$\frac{c}{a}$��
��ã�a=2��
����ԲM�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1��
��2��������������ͼ������ͼ��
��C��2cos�ȣ�sin�ȣ���F��-2��y����
��|DC|=|CE|����E��2cos�ȣ�2sin�ȣ���
���E����ABΪֱ����Բ�ϣ�
��B��E��F���㹲�ߣ�
��$\frac{2sin��-0}{2cos��-2}$=$\frac{y-0}{-2-2}$��
��y=4$\frac{sin��}{1-cos��}$��
�ʵ�F��-2��4$\frac{sin��}{1-cos��}$����G��-2��2$\frac{sin��}{1-cos��}$����
$\overrightarrow{EG}$=��-2-2cos�ȣ�2$\frac{sin��}{1-cos��}$-2sin�ȣ���$\overrightarrow{OE}$=��2cos�ȣ�2sin�ȣ���
��$\overrightarrow{EG}$•$\overrightarrow{OE}$=��-2-2cos�ȣ�2cos��+��2$\frac{sin��}{1-cos��}$-2sin�ȣ�2sin��
=-4cos��-4cos2��+4$\frac{si{n}^{2}��cos��}{1-cos��}$=-4cos��-4cos2��+4cos�ȣ�1+cos�ȣ�=0��
��ֱ��GE����ABΪֱ����Բ�����ߣ�
���� ���⿼����Բ���ߵ�Ӧ�ü�ƽ��������Ӧ�ã�ͬʱ������ֱ����Բ��λ�ù�ϵ��Ӧ�ã�ע�����ν�ϵ�Ӧ�ã������е��⣮


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
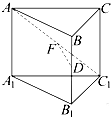 ���ⳤ����ȵ���������ABC-A1B1C1�У�DΪBB1���е㣬F��AC1�ϣ���DF��AC1�����������ۣ���AC1��BC����AF=FC1����ƽ��DAC1��ƽ��ACC1A1��������ȷ�ĸ���Ϊ��������
���ⳤ����ȵ���������ABC-A1B1C1�У�DΪBB1���е㣬F��AC1�ϣ���DF��AC1�����������ۣ���AC1��BC����AF=FC1����ƽ��DAC1��ƽ��ACC1A1��������ȷ�ĸ���Ϊ��������| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-$\frac{1}{e}$ | B�� | a��-$\frac{1}{e}$ | C�� | a��-$\frac{1}{2}$ | D�� | a��-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | �ϼ� | |
| �� | 20 | 5 | 25 |
| �� | 10 | 15 | 25 |
| �ϼ� | 30 | 20 | 50 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com