
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 则
则 ”类比“若
”类比“若 为三个向量则
为三个向量则 ”
” 中,
中, 猜想
猜想
 ,则
,则 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
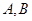 为两个不同的定点,动点
为两个不同的定点,动点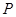 满足
满足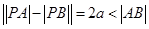 ,得点
,得点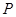 的轨迹为双曲线
的轨迹为双曲线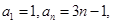 ,求出
,求出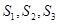 猜想出数列
猜想出数列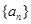 的前
的前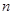 项和
项和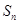 的表达式
的表达式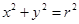 的面积
的面积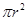 ,猜想出椭圆
,猜想出椭圆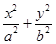 =1的面积
=1的面积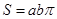
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
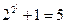 ;
;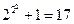 ;
;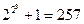 ;
;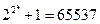 ,于是该数学家猜想:任何形如
,于是该数学家猜想:任何形如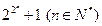 都是质数,请判断该数学家的推理方式并对该结论给出正误判断( ).
都是质数,请判断该数学家的推理方式并对该结论给出正误判断( ).| A.类比推理推理结果正确 | B.类比推理推理结果错误 |
| C.归纳推理推理结果正确 | D.归纳推理推理结果错误 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
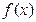 定义域中任意的
定义域中任意的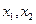 (
(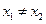 ),有如下结论:
),有如下结论: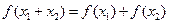 ;(2)
;(2)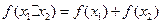 ;
;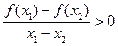 ;(4)
;(4)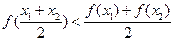 ;试分别写出对应上述一个结论成立的四个函数:
;试分别写出对应上述一个结论成立的四个函数:查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
| B.在△ABC中,“A>B”是“sinA>sinB”的充分不必要条件 |
C.“ ”恒成立的充要条件是“ ”恒成立的充要条件是“ ” ” |
D.若 、 、 是直线, 是直线, 是平面, 是平面, 平面 平面 ,那么:“ ,那么:“ ”是“ ”是“ ”的充要条件 ”的充要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com