
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
分析 由f(x)为偶函数,可得t=0,讨论x>0时,f(x)递增,化a=f(log0.30.25),运用指数函数和对数函数的单调性,比较π1.5、2、log0.30.25的大小,即可得到a,b,c的大小关系.
解答 解:函数f(x)=log3|x-t|是偶函数,
可得f(-x)=f(x),即log3|-x-t|=log3|x-t|,
即有|-x-t|=|x-t|恒成立,可得t=0,
则f(x)=log3|x|,当x>0时,f(x)=log3x为增函数,
a=f(log0.34)=f(log0.30.25),c=f(2-t)=f(2),
由1<log0.30.25<2,π1.5>π>3,
即有π1.5>2>log0.30.25,
则f(π1.5)>f(2)>f(log0.30.25),
即为b>c>a.
故选:A.
点评 本题考查函数的奇偶性和单调性的判断和应用:比较大小,注意运用定义法和转化思想,同时考查指数函数和对数函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -270 | B. | 270 | C. | -90 | D. | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
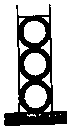 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,e) | B. | (e,10] | C. | (1,10] | D. | (10,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com