
【题目】正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
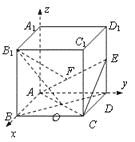
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点F 在EA 上且B1F⊥AE,试求点F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() (Ⅲ)
(Ⅲ) ![]()
【解析】
证明:(I) 由题设知下列各点的坐标A(0, 0, 0),B(2, 0, 0),C (2, 2, 0),
D (0, 2, 0),E (0, 2, 1),B1(2, 0, 2).
∵O是正方形ABCD的中心,∴O (1, 1, 0).
∴![]() = (-1, 1, -2),
= (-1, 1, -2),![]() = (2, 2, 0),
= (2, 2, 0),![]() = (0,2, 1).
= (0,2, 1).
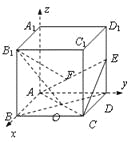
∴·![]() = (-1, 1, -2)·(2, 2, 0)
= (-1, 1, -2)·(2, 2, 0)
= -1·2 + 1·2-2·0 = 0.
![]() ·= (-1, 1, -2)·(0, 2, 1)
·= (-1, 1, -2)·(0, 2, 1)
= -1·0 + 1·2-2·1 = 0.
∴![]()
即B1O ⊥AC,B1O⊥AE,
∴B1O⊥平面ACE.
(II) 由F点在AE上,可设点F的坐标为F (0, 2l,l),
则![]() = (-2, 2l,l-2).
= (-2, 2l,l-2).
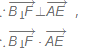
= (-2, 2l,l-2)·(0, 2, 1) = 5l-2 = 0,
∴l= ![]() ,
,
∴![]() .
.
(III) ∵B1O⊥平面EAC,B1F⊥AE,连结OF,由三垂线定理的逆定理得OF⊥AE.
∴∠OFB1即为二面角B1-EA-C的平面角.
∴![]() =
= ![]()
又![]() =
=![]() ,
,
∴![]() =
= 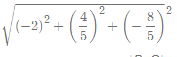 =
= ![]() .
.
在Rt△B1OF中,sin∠B1FO= ![]() =
= ![]() .
.
故二面角B1-EA-C的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】众所周知,城市公交车的数量太多会造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的50名候车乘客中随机抽取10名,统计了他们的候车时间(单位:分钟),得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估计这10名乘客的平均候车时间(同一组中的每个数据可用该组区间的中点值代替);
(2)估计这50名乘客的候车时间少于10分钟的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知数列![]() 为等差数列,其前n项和为
为等差数列,其前n项和为![]() .若
.若![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小关系.
的大小关系.
(2)已知数列![]() 为等差数列,
为等差数列,![]() 的前n项和为
的前n项和为![]() .证明:若存在正整数k,使
.证明:若存在正整数k,使![]() ,则
,则![]() .
.
(3)在等比数列![]() 中,设
中,设![]() 的前n项乘积
的前n项乘积![]() ,类比(2)的结论,写出一个与
,类比(2)的结论,写出一个与![]() 有关的类似的真命题,并证明.
有关的类似的真命题,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
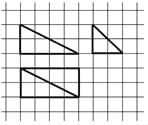
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
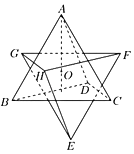
【题目】正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
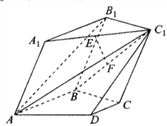
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
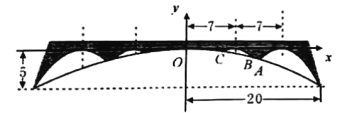
【题目】早在一千多年之前,我国已经把溢流孔用于造桥技术,以减轻桥身重量和水流对桥身的冲击,现设桥拱上有如图所示的4个溢流孔,桥拱和溢流孔轮廓线均为抛物线的一部分,且四个溢流孔轮廓线相同.根据图上尺寸,在平面直角坐标系![]() 中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点
中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com