
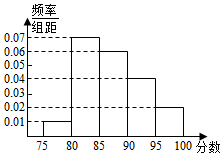
 2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.分析 (Ⅰ)由频率分布直方图能求出第3,4,5组的频率.
(2)分别求出第3,4,5组的人数,再利用分层抽样的方法在60名学生中抽取6名学生,能求出每组抽取的人数.
(3)在这6名学生中随机抽取2名学生接受学校组织模拟考官的面试,先求出基本事件总数,第4组至少有一名学校被考官面试的对立事件是第4组没有学生被考官面试,由此利用对立事件概率计算公式能求出第4组至少有一名学校被考官面试的概率.
解答 解:(Ⅰ)由题意,第3组的频率为0.06×5=0.3,
第4组的频率为0.04×5=0.2,
第5组的频率为0.02×5=0.1.
(2)第3组的人数为0.3×100=30人,
第4组的人数为0.2×100=20人,
第5组的人数为0.1×100=10人,
∵第3,4,5组共有60名学生,
∴利用分层抽样的方法在60名学生中抽取6名学生,每组抽取的人数分别为:
第3组:$\frac{30}{60}×6=3$人,
第4组:$\frac{20}{60}×6=2$人,
第5组:$\frac{10}{60}×6=1$人,
∴在第3,4,5组分别抽取3人、2人,1人.
(3)在这6名学生中随机抽取2名学生接受学校组织模拟考官的面试,
基本事件总数n=${C}_{6}^{2}$=15,
第4组至少有一名学校被考官面试的对立事件是第4组没有学生被考官面试,
∴第4组至少有一名学校被考官面试的概率:
p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{3}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月收入(元) | [1500,2500) | [2500,3500) | [3500,4500) | [4500,5500) | [5500,6500) | [6500,7500) |
| 频数 | 5 | 10 | 14 | 11 | 6 | 4 |
| 反对人数 | 4 | 8 | 11 | 6 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|2≤x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | 1 | 2 | 3 | 4 | 5 |
| 男生 | 1 | 4 | 3 | 2 | 2 |
| 女生 | 0 | 1 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com