
分析 (1)去掉绝对值,求出a的范围即可;
(2)根据基本不等式的性质求出m、n的值即可,设g(x)=|x-3|-f(x),通过讨论x的范围,得到g(x)的最大值,从而求出Aa的范围即可.
解答 解:(1)|3x+a|-a≤6,-a-6≤3x+a≤a+6,
$-\frac{2}{3}a-2≤x≤2$,
$-1≤-\frac{2a}{3}-2≤2$,
-6≤a≤-$\frac{3}{2}$;
(2)∵$m+n=1(m,n>0),\frac{1}{m}+\frac{1}{n}=(m+n)(\frac{1}{m}+\frac{1}{n})=2+\frac{n}{m}+\frac{m}{n}≥2\sqrt{\frac{n}{m}×\frac{m}{n}}+2=4$,
当且仅当$m=n=\frac{1}{2}$时,取等号;
设g(x)=|x-3|-f(x)=|x-3|-|3x+a|+a=$\left\{{\begin{array}{l}{2x+3+2a,x<-\frac{a}{3}}\\{-4x+3,-\frac{a}{3}≤x≤3}\\{-2x-3,x>3}\end{array}}\right.$,
根据图象可知当$x=-\frac{a}{3}$取最大值,$g(-\frac{a}{3})≤4$,即$-4×(-\frac{a}{3})+3≤4⇒0<a≤\frac{3}{4}$,
所以a的取值范围为:0<a≤$\frac{3}{4}$.
点评 本题考查了解绝对值不等式问题,考查基本不等式的性质以及函数恒成立问题,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x2+$\frac{{y}^{2}}{3}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | y2+$\frac{{x}^{2}}{3}$=1 | D. | y2-$\frac{{x}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,5,6} | B. | {5,6} | C. | {4,6} | D. | {x|4<x≤6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | $(\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1-\frac{1}{e}$ | B. | $\frac{e+1}{e^2}$ | C. | $\frac{1}{e}$ | D. | $\frac{e-1}{e^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sin1)<f(cos1) | B. | f(sin1)=f(cos1) | C. | f(sin1)>f(cos1) | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
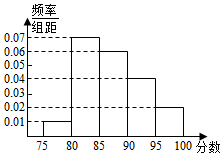 2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com