
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | $(\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})$ |
分析 直线x+y+m=0得直线斜率k=-1,若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,则等价为f′(x)≠-1,恒成立,解不等式即可得实数a的取值范围.
解答 解:函数的导数f′(x)=3x2-3a≥-3a,
若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,则直线的斜率为-1,
等价为f(x)′=3x2-3a≠-1,
又抛物线开口向上则必在直线上面,即最小值大于直线斜率,
则当x=0时取最小值,-3a>-1,
则a的取值范围为a<$\frac{1}{3}$,
故实数a的取值范围是(-∞,$\frac{1}{3}$),
故选:D
点评 本题主要考查导数的几何意义,利用一元二次函数的性质是解决本题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
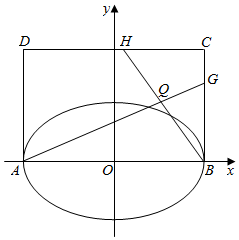 如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.
如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
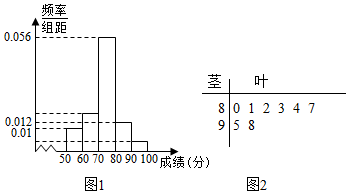
 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|2≤x<5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com