
如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.
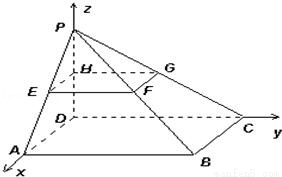
E(a,0,b),F(a,a,b),G(0,a,b),H(0,0,b)
【解析】
试题分析:根据条件建空间直角立坐标系,根据E,F,G,H分别为侧棱中点,得到这4个点的竖坐标都为P的竖坐标的一半,E在底面面上的投影为AD中点,得到E的坐标,F在坐标平面xOz和yOz上的投影分别为点E和G得到F与E横坐标相同,得到结果.
【解析】
由图形知,DA⊥DC,DC⊥DP,DP⊥DA,故以D为原点,建立如图空间坐标系D﹣xyz.
∵E,F,G,H分别为侧棱中点,由立体几何知识可知,平面EFGH与底面ABCD平行,
从而这4个点的竖坐标都为P的竖坐标的一半,也就是b,
由H为DP中点,得H(0,0,b)
E在底面面上的投影为AD中点,
∴E的横坐标和纵坐标分别为a和0,
∴E(a,0,b),
同理G(0,a,b);
F在坐标平面xOz和yOz上的投影分别为点E和G,
∴F与E横坐标相同都是a,
与G的纵坐标也同为a,又F竖坐标为b,
∴F(a,a,b).


科目:高中数学 来源:[同步]2015年北师大版必修三 1.8 最小二乘估计练习卷(解析版) 题型:选择题
下列叙述中( )
①变量间关系有函数关系,还有相关关系;
②回归函数即用函数关系近似地描述相互关系;
③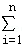 xi=x1+x2+…+xn;
xi=x1+x2+…+xn;
④线性回归方程y=bx+a中,b=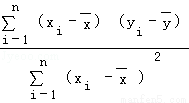 ,a=
,a=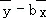 ;
;
⑤线性回归方程一定可以近似地表示所有相关关系.其中正确的有( )
A.①②③ B.①②③④⑤ C.①②③④ D.③④⑤
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修4-5 3.1 数学归纳法原理练习卷(解析版) 题型:填空题
设数列{ }前n项和为Sn,则S1= ,S2= ,S3= ,S4= ,并由此猜想出Sn= .
}前n项和为Sn,则S1= ,S2= ,S3= ,S4= ,并由此猜想出Sn= .
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修1-2 1.2回归分析练习卷(解析版) 题型:选择题
下列结论正确的是( )
①函数关系是一种确定性关系;
②相关关系是一种非确定性关系;
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;
④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
A.①② B.①②③ C.①②④ D.①②③④
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版必修二2.4 空间直角坐标系练习卷(解析版) 题型:填空题
如图,棱长为3a正方体OABC﹣D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版必修二2.4 空间直角坐标系练习卷(解析版) 题型:选择题
设A(3,3,1)、B(1,0,5)、C(0,1,0),则AB的中点M到C点的距离为( )
A. B.
B.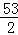 C.
C.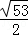 D.
D.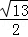
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版必修二2.1平面直角坐标系中的基本公式练习卷(解析版) 题型:选择题
已知点A(x,5)关于点(1,y)的对称点(﹣2,﹣3),则点P(x,y)到原点的距离是( )
A.4 B.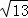 C.
C.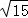 D.
D.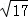
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷(解析版) 题型:
已知点A(﹣3,1,﹣4),则点A关于x轴的对称点的坐标为( )
A.(﹣3,﹣1,4) B.(﹣3,﹣1,﹣4)
C.(3,1,4) D.(3,﹣1,﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com