
分析 (1)∵椭圆C1:$\frac{x^2}{a^2}$+$\frac{y^2}{3}$=1(a>$\sqrt{3}$)的离心率为$\frac{1}{2}$,求出椭圆的标准方程,进而求出焦点坐标,可得抛物线C2的方程;
(2)求出直线与抛物线的交点坐标,利用对称法,可得△ABD周长c的最小值.
解答 解:(1)∵椭圆C1:$\frac{x^2}{a^2}$+$\frac{y^2}{3}$=1(a>$\sqrt{3}$)的离心率为$\frac{1}{2}$,
∴$\frac{{a}^{2}-3}{{a}^{2}}=\frac{1}{4}$,解得:a2=4,
∴c2=a2-3=1,
即椭圆C1:$\frac{{x}^{2}}{4}$+$\frac{y^2}{3}$=1的右焦点F坐标为(1,0),
∵抛物线C2:y2=2px(p>0)的焦点F是椭圆C1的右焦点.
∴$\frac{p}{2}$=1,即p=2,
∴抛物线C2的方程为:y2=4x
(2)过点F且倾斜角为$\frac{π}{3}$的直线l方程为:y=$\sqrt{3}$(x-1),
由$\left\{\begin{array}{l}{y}^{2}=4x\\ y=\sqrt{3}(x-1)\end{array}\right.$得:3x2-10x+3=0,
解得:$\left\{\begin{array}{l}x=\frac{1}{3}\\ y=-\frac{2\sqrt{3}}{3}\end{array}\right.$,或$\left\{\begin{array}{l}x=3\\ y=2\sqrt{3}\end{array}\right.$,
∴A($\frac{1}{3}$,$-\frac{2\sqrt{3}}{3}$),B(3,2$\sqrt{3}$),
∴|AB|=$\frac{16}{3}$,
A点关于直线x=2为对称点为A′(-$\frac{13}{3}$,$-\frac{2\sqrt{3}}{3}$),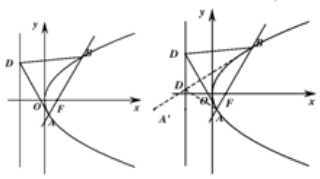
∴c=|AD|+|BD|+|AB|
=|A′D|+|BD|+|AB|
≥|A′B|+|AB|
=$\frac{26}{3}$+$\frac{16}{3}$=14,
∴△ABD周长c的最小值为14.
点评 本题考查的知识点是椭圆的简单性质,抛物线和椭圆的标准方程,直线与圆锥曲线的位置关系,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{5}$) | B. | (-$\sqrt{5}$,0) | C. | (-$\sqrt{13}$,0) | D. | (0,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第1组 | 2 | 2 | 第13组 | 5 | 6 | 第25组 | 2 | 6 |
| 第2组 | 6 | 5 | 第14组 | 1 | 4 | 第62组 | 6 | 3 |
| 第3组 | 1 | 3 | 第15组 | 2 | 3 | 第27组 | 6 | 6 |
| 第4组 | 5 | 3 | 第16组 | 5 | 2 | 第28组 | 1 | 2 |
| 第5组 | 5 | 2 | 第17组 | 1 | 6 | 第29组 | 6 | 1 |
| 第6组 | 4 | 5 | 第18组 | 4 | 6 | 第30组 | 4 | 1 |
| 第7组 | 3 | 4 | 第19组 | 3 | 1 | 第31组 | 3 | 6 |
| 第8组 | 6 | 5 | 第20组 | 4 | 2 | 第32组 | 4 | 3 |
| 第9组 | 3 | 4 | 第21组 | 3 | 3 | 第33组 | 5 | 6 |
| 第10组 | 6 | 4 | 第22组 | 4 | 4 | 第34组 | 1 | 6 |
| 第11组 | 1 | 2 | 第23组 | 6 | 2 | 第35组 | 4 | 2 |
| 第12组 | 1 | 5 | 第24组 | 5 | 2 | 第36组 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
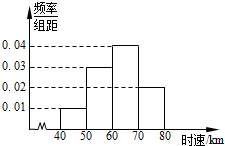 为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.
为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com