分析:(1)由题意,ABCD-A1B1C1D1是底面边长为1的正四棱柱,则AB1与底面A1B1C1D1所成角即为∠AB1A1,则AB1的长度可求,进而可求该棱柱的侧面积;
(2)由图形借助面面垂直找到点C在平面AB1D1的位置,利用三角形的相似解出.
(3)由高AA1=2,ABCD-A1B1C1D1是底面边长为1的正四棱柱,则可得三棱锥A-A1B1D1的体积,而四面体AB1D1C的体积为正四棱柱ABCD-A1B1C1D1的体积减去四个三棱锥A-A1B1D1的体积,故四面体AB1D1C的体积可求.
解答:解:(1)由于ABCD-A
1B
1C
1D
1是底面边长1正四棱柱,则AB
1与底面A
1B
1C
1D
1所成的角为∠AB
1A
1,
又由AB
1与底面A
1B
1C
1D
1所成的角为
arctan,则
tan∠AB1A1==
,故
AA1=则该棱柱的侧面积为
4×1×=2.
(2)∵O
1为B
1D
1的中点,而△AB
1D
1是以B
1D
1为底边的等腰三角形,
∴AO
1⊥B
1D
1∴B
1D
1⊥平面ACC
1A
1∴平面AB
1D
1⊥平面ACC
1A
1且交线为AO
1,
∴点C到平面AB
1D
1的投影点必落在A0
1上即垂足H,
在矩形AA
1C
1C中,利用R
t△AA
1O
1∽R
t△CHA 得到
=而
AH ==∴
=?
=,则AA
1=2,
故正四棱柱ABCD-A
1B
1C
1D
1的体积V=1×1×2=2.
(3)由于ABCD-A
1B
1C
1D
1是底面边长为1的正四棱柱,高AA
1=2,
则三棱锥A-A
1B
1D
1的体积为
××A1B1×A1D1×AA1=,
又由四面体AB
1D
1C的体积为正四棱柱ABCD-A
1B
1C
1D
1的体积减去四个三棱锥A-A
1B
1D
1的体积
则四面体AB
1D
1C的体积为
2×1×1-4×=,
故四面体AB
1D
1C的体积为
.
点评:本小题主要考查空间线面关系、线面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

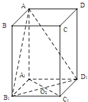 已知ABCD-A1B1C1D1是底面边长1正四棱柱,O1为A1C1与B1D1的交点.
已知ABCD-A1B1C1D1是底面边长1正四棱柱,O1为A1C1与B1D1的交点.

 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.