
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数p,使其值域为
上单调递减;②存在常数p,使其值域为![]() ,则称函数
,则称函数![]() 为
为![]() 的“渐近函数”;
的“渐近函数”;
(1)证明:函数![]() 是函数
是函数![]()
![]() 的渐近函数,并求此时实数p的值;
的渐近函数,并求此时实数p的值;
(2)若函数![]()
![]()
![]() ,证明:当
,证明:当![]() 时,
时,![]() 不是
不是![]() 的渐近函数.
的渐近函数.
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动(向右为顺时针,向左为逆时针).设顶点
轴滚动(向右为顺时针,向左为逆时针).设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则关于
,则关于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得![]() 分).设每次击鼓出现音乐的概率为
分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 恒过
恒过![]() 的一个焦点
的一个焦点![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的顶点均在
的顶点均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直线
,若直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,求直线
,求直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在y轴上截得的弦MN的长为8.
,且在y轴上截得的弦MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点![]() ,长为
,长为![]() 的线段PQ的两端点在轨迹C上滑动.当
的线段PQ的两端点在轨迹C上滑动.当![]() 轴是
轴是![]() 的角平分线时,求直线PQ的方程.
的角平分线时,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
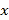
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式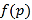 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com