函数f(x)=x2+ax+3,x∈[0,2]
(Ⅰ)若a=2,求f(x)的最值,并说明当f(x)取最值时的x的值;
(Ⅱ)若f(x)≥0恒成立,求a的取值范围.
解:(Ⅰ)当a=2时,函数f(x)=x
2+2x+3=(x+1)
2+2,
由于f (x)的对称轴为x=-1,f (x)在[0,2]上是增函数,…(1分)
故当x=0时,f(x)
min=f(0)=3;…(3分)
当x=2时,f(x)
max=f(2)=11.…(5分)
(Ⅱ)[法一]:若f(x)≥0恒成立,即x
2+ax+3≥0对于x∈[0,2]恒成立,故f(x)=x
2+ax+3的最小值大于或等于零.
结合二次函数f(x)=x
2+ax+3的图象与性质得:△=a
2-4×3≤0,或
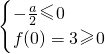
,或
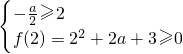
. …(9分)
解得
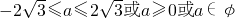
,…(11分)
所以a得取值范围是
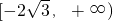
.…(12分)
法二:当x=0时,可得a∈R,当x∈(0,2]时,可得
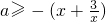
,令
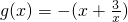
,由于
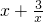
≥2

,当且仅当x=

时,取等号.
故有-(
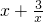
)≤-2

,故
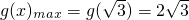
,从而,
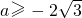
.
分析:(Ⅰ)当a=2时,函数f(x)=x
2+2x+3=(x+1)
2+2,由于f (x)的对称轴为x=-1,f (x)在[0,2]上是增函数,由此求得f(x)的最值,以及f(x)取最值时的x的值.
(Ⅱ)[法一]:由题意可得 x
2+ax+3≥0对于x∈[0,2]恒成立,故f(x)=x
2+ax+3的最小值大于或等于零,结合二次函数f(x)=x
2+ax+3的图象与性质,求得a的取值范围.
法二:当x=0时,可得a∈R,满足条件.当x∈(0,2]时,可得
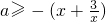
,令
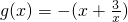
,利用基本不等式求得g(x)的最大值,即可得到a的取值范围.
点评:本题主要考查二次函数的性质,函数的恒成立问题,求二次函数在闭区间上的最值,属于中档题.

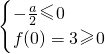 ,或
,或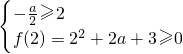 . …(9分)
. …(9分)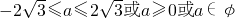 ,…(11分)
,…(11分)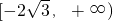 .…(12分)
.…(12分)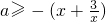 ,令
,令 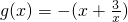 ,由于
,由于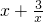 ≥2
≥2 ,当且仅当x=
,当且仅当x= 时,取等号.
时,取等号.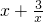 )≤-2
)≤-2 ,故
,故 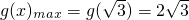 ,从而,
,从而,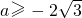 .
.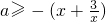 ,令
,令 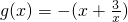 ,利用基本不等式求得g(x)的最大值,即可得到a的取值范围.
,利用基本不等式求得g(x)的最大值,即可得到a的取值范围.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案