
已知函数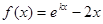 (
(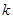 为非零常数).
为非零常数).
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;
(Ⅱ)若
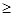
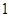 恒成立,求
恒成立,求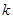 的值;
的值;
(Ⅲ)对于 增区间内的三个实数
增区间内的三个实数 (其中
(其中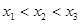 ),
),
证明: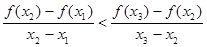 .
.
(Ⅰ)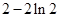 (Ⅱ)
(Ⅱ)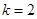 (Ⅲ)由已知得:,
(Ⅲ)由已知得:,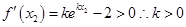
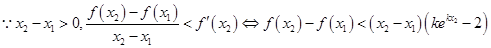
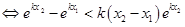
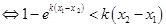
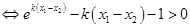 . 设
. 设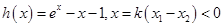
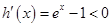 ,
,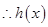 在
在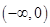 内是减函数,
内是减函数,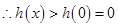 ,即
,即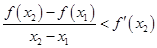 同理
同理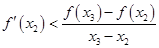 ,∴
,∴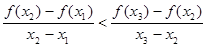
【解析】
试题分析:(Ⅰ)由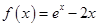 ,得
,得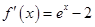 , 1分
, 1分
令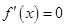 ,得
,得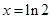 . 当
. 当 ,
,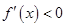 知
知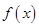 在
在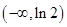 单调递减;
单调递减;
当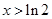 ,
,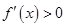 知
知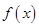 在
在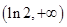 单调递增;
单调递增;
故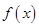 的最小值为
的最小值为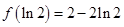 . 4分
. 4分
(Ⅱ)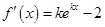 ,当
,当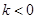 时,
时, 恒小于零,
恒小于零,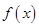 单调递减.
单调递减.
当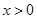 时,
时,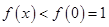 ,不符合题意. 5分
,不符合题意. 5分
对于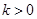 ,由
,由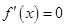 得
得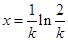
当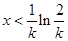 时,
时,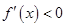 ,∴
,∴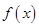 在
在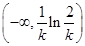 单调递减;
单调递减;
当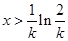 时,
时,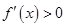 ,∴
,∴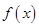 在
在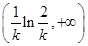 单调递增;
单调递增;
于是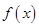 的最小值为
的最小值为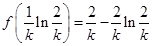 . 7分
. 7分
只需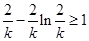 成立即可,构造函数
成立即可,构造函数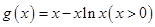 .
.
∵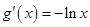 ,∴
,∴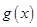 在
在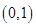 上单调递增,在
上单调递增,在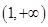 上单调递减,
上单调递减,
则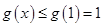 ,仅当
,仅当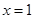 时取得最大值,故
时取得最大值,故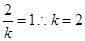 9分
9分
(Ⅲ)由已知得:,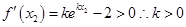
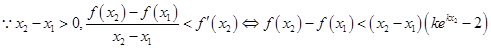
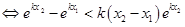
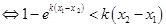
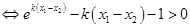 . 设
. 设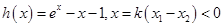
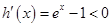 ,
,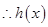 在
在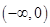 内是减函数,
内是减函数,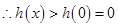 ,即
,即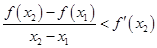 同理
同理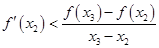 ,∴
,∴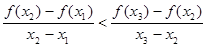
考点:函数单调性最值
点评:求函数最值要结合函数的单调区间确定最值点位置,第二问中不等式恒成立求参数范围常采用分离参数法转化为求函数最值问题,第三问将证明不等式转化为求函数最值


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| m | x-1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| m |
| x-1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省合肥六中高一(上)期中数学试卷(解析版) 题型:解答题
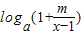 (a>0且a≠1)为奇函数.
(a>0且a≠1)为奇函数.查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省高三第二次月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知函数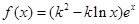 (
(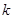 为非零常数,
为非零常数,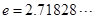 是自然对数的底数),曲线
是自然对数的底数),曲线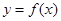 在点
在点 处的切线与
处的切线与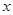 轴平行.
轴平行.
(1)判断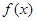 的单调性;
的单调性;
(2)若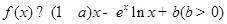 , 求
, 求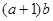 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com