
| A. | f(x)=$\frac{|x|}{x}$ | B. | f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$<x<$\frac{π}{2}$) | ||
| C. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | D. | f(x)=x2ln(x2+1) |
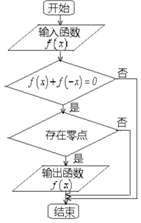
分析 模拟执行程序框图可得其功能是输出的函数为奇函数,并且此函数存在零点,一一验证即可.
解答 解:根据程序框图可知输出的函数为奇函数,并且此函数存在零点,经验证:f(x)=$\frac{|x|}{x}$不存在零点;
f(x)=$\frac{cosx}{x}$不存在零点;f(x)=x2ln(x2+1)为偶函数,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$的定义域为全体实数,且f(-x)=-f(x),故此函数为奇函数,且令f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$=0,得x=0,函数f(x)存在零点,
故选:C.
点评 本题主要考查了程序框图和算法,考查了函数的性质及其应用,属于基础题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
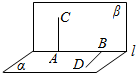 如图,已知α∩β=l,A∈l,B∈l,(A,B不重合),过A在平面α内做直线AC,过B在平面α内做直线BD.求证:AC,BD是异面直线.
如图,已知α∩β=l,A∈l,B∈l,(A,B不重合),过A在平面α内做直线AC,过B在平面α内做直线BD.求证:AC,BD是异面直线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com