
【题目】已知 ![]() ,0<β<
,0<β< ![]() ,cos(
,cos( ![]() +α)=﹣
+α)=﹣ ![]() ,sin(
,sin( ![]() +β)=
+β)= ![]() ,求sin(α+β)的值.
,求sin(α+β)的值.
【答案】解:∵ ![]() <α<
<α< ![]() ,∴
,∴ ![]() <
< ![]() +α<π.
+α<π.
又cos( ![]() +α)=﹣
+α)=﹣ ![]() ,∴sin(
,∴sin( ![]() +α)=
+α)= ![]() .
.
又∵0<β< ![]() ,∴
,∴ ![]() <
< ![]() +β<π.
+β<π.
又sin( ![]() +β)=
+β)= ![]() ,∴cos(
,∴cos( ![]() +β)=﹣
+β)=﹣ ![]() ,
,
∴sin(α+β)=﹣sin[π+(α+β)]=﹣sin[( ![]() +α)+(
+α)+( ![]() +β)]
+β)]
=﹣[sin( ![]() +α)cos(
+α)cos( ![]() +β)+cos(
+β)+cos( ![]() +α)sin(
+α)sin( ![]() +β)]
+β)]
=﹣[ ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() ]=
]= ![]() .
.
所以sin(α+β)的值为: ![]() .
.
【解析】根据α、β的范围,确定 ![]() +α、
+α、 ![]() +β的范围,求出sin(
+β的范围,求出sin( ![]() +α)、cos(
+α)、cos( ![]() +β)的值,利用sin(α+β)=﹣sin[π+(α+β)]=﹣sin[(
+β)的值,利用sin(α+β)=﹣sin[π+(α+β)]=﹣sin[( ![]() +α)+(
+α)+( ![]() +β)],展开,然后求出它的值即可.
+β)],展开,然后求出它的值即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a2=6,a2+a3=24,在等差数列{bn}中,b1=a1 , b3=﹣10.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点,其中
两点,其中![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).
).
(I)求椭圆C的方程;
(Ⅱ)设与圆O:x2+y2=![]() 相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
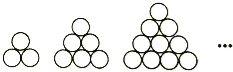
【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.问底子(每层三角形边茭草束数,等价于层数)几何?”中探讨了“垛枳术”中的落一形垛(“落一形”即是指顶上1束,下一层3束,再下一层6束,…,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层茭草束数),则本问题中三角垛底层茭草总束数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.
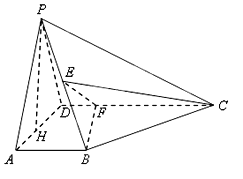
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com