
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=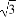 AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.

(1)求证:AE⊥平面SBD.
(2)M,N分别为线段SB,CD上的点,是否存在M,N,使MN⊥CD且MN⊥SB,若存在,确定M,N的位置;若不存在,说明理由.
(1)见解析 (2) 存在,理由见解析
【解析】(1)因为四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,
所以SD⊥平面ABCD.
BD就是SB在底面ABCD上的射影.
∵AB=2AD,E为CD上一点,且CE=3DE.
∴tan∠DAE=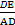 =
=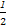 ,tan∠DBA=
,tan∠DBA=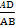 =
=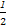 ,
,
∴∠DAE=∠DBA,同理∠BDA=∠AED,
∴∠DAE+∠BDA=90°.
∴AE⊥BD,∴AE⊥SB.∵SB∩BD=B,
∴AE⊥平面SBD.
(2)假设存在MN满足MN⊥CD且MN⊥SB.
建立如图所示的空间直角坐标系,

由题意可知,D(0,0,0),A(a,0,0),C(0,2a,0),B(a,2a,0),S(0,0,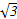 a),
a),
设 =
= +t
+t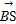 =(a,2a,0)+t(-a,-2a,
=(a,2a,0)+t(-a,-2a,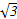 a)=(a-ta,2a-2ta,
a)=(a-ta,2a-2ta,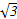 ta)(t∈[0,1]),
ta)(t∈[0,1]),
即M (a-ta,2a-2ta,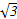 ta),N(0,y,0),y∈[0,2a],
ta),N(0,y,0),y∈[0,2a],
 =(a-ta,2a-2ta-y,
=(a-ta,2a-2ta-y,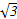 ta).
ta).
使MN⊥CD且MN⊥SB,
则

可得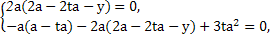
t=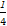 ∈[0,1],y=
∈[0,1],y=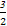 a∈[0,2a].
a∈[0,2a].
故存在MN使MN⊥CD且MN⊥SB.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:选择题
给出下列四个命题:
①?α∈R,sinα+cosα>-1;
②?α∈R,sinα+cosα= ;
;
③?α∈R,sinαcosα≤ ;
;
④?α∈R,sinαcosα=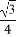 .
.
其中正确命题的序号是( )
(A)①② (B)①③ (C)③④ (D)②④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:解答题
直三棱柱ABC-A1B1C1的底面为等腰直角三角形,∠BAC=90°,AB=AC=2,AA1=2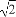 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.
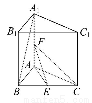
求(1)异面直线EF和A1B所成的角.
(2)三棱锥A-EFC的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
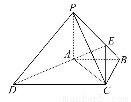
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
(A)0个 (B)1个 (C)2个 (D)3个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:填空题
已知l∥α,且l的方向向量为u=(2,m,1),平面α的法向量为v=(1, ,2),则m= .
,2),则m= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于( )
(A)2 (B)-4 (C)4 (D)-2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
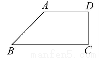
一个水平放置的平面图形的斜二测直观图是直角梯形 (如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
(A) +
+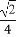 (B)2+
(B)2+
(C) +
+ (D)
(D) +
+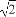
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( )
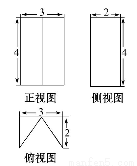
(A)16 (B)12 (C)8 (D)6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com