
 和
和 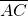 夹角平分线上的一点,且
夹角平分线上的一点,且 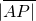 =2,则
=2,则 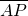 的坐标是
的坐标是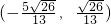
 ,
, )
)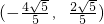
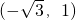
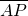 的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由|
的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由| |=
|= =2,求得x、y的值,即可得到
=2,求得x、y的值,即可得到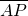 的坐标.
的坐标. =(-6,-4),
=(-6,-4), =(-2,3),∠BAP=∠CAP,
=(-2,3),∠BAP=∠CAP,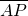 的坐标为(x,y),而由两个向量的夹角公式可得
的坐标为(x,y),而由两个向量的夹角公式可得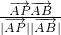 =
=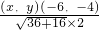 =
=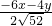 ,
,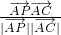 =
=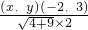 =
=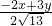 ,
,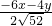 =
=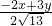 >0,解得 x=-5y<0.
>0,解得 x=-5y<0. |=
|= =2,可得 x=-5
=2,可得 x=-5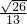 ,y=
,y=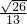 ,故
,故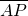 的坐标是
的坐标是 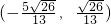 ,
,

科目:高中数学 来源: 题型:
| ||
| 7 |
| ||
| 7 |
| MA |
| MB |
| MC |
| 0 |
| NC |
| 7 |
| NA |
| 7 |
| NB |
| MN |
| AB |
| PE |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| AB |
. |
| AC |
. |
| AP| |
. |
| AP |
查看答案和解析>>
科目:高中数学 来源:必修二训练数学北师版 北师版 题型:044
在直角坐标中,△ABC的三个顶点是A(0,3),B(3,3),C(2,0),若直线x=a,将△ABC分割成面积相等的两部分,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com