
| A. | [$\frac{3}{5}$,$\frac{7}{5}$] | B. | [$\frac{3}{5}$,$\frac{9}{5}$] | C. | [$\frac{7}{5}$,$\frac{9}{5}$] | D. | [$\frac{3}{5}$,$\frac{11}{5}$] |
分析 如图所示,动点P(x,y)满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y+1≥x}\\{x+y≤3}\end{array}\right.$,即阴影△BCD.于是向量$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影=$\frac{|\overrightarrow{OP}•\overrightarrow{OA}|}{|\overrightarrow{OA}|}$=$\frac{|3x+4y|}{5}$,设3x+4y=t,1≤x≤2.化为直线l:y=$-\frac{3}{4}x$+$\frac{t}{4}$,当直线l经过点B时,可得t=3;当直线l经过点D时,可得t=11.可得t的范围.即可得出向量$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影范围.
解答 解:如图所示,
动点P(x,y)满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y+1≥x}\\{x+y≤3}\end{array}\right.$,即阴影△BCD.
B(1,0),C(2,1),D(1,2).
∴向量$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影=$\frac{|\overrightarrow{OP}•\overrightarrow{OA}|}{|\overrightarrow{OA}|}$=$\frac{|3x+4y|}{5}$,
设3x+4y=t,1≤x≤2.
化为直线l:y=$-\frac{3}{4}x$+$\frac{t}{4}$,
当直线l经过点B时,可得t=3;
当直线l经过点D时,可得t=11.
∴3≤t≤11.
∴向量$\overrightarrow{OP}$在$\overrightarrow{OA}$上的投影=$\frac{|3x+4y|}{5}$∈$[\frac{3}{5},\frac{11}{5}]$.
故选:D.
点评 本题考查了向量数量积运算性质、向量投影、线性规划有关知识,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -5 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
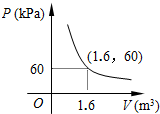 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$m3 | B. | 小于$\frac{5}{4}$m3 | C. | 不小于$\frac{4}{5}$m3 | D. | 不大于$\frac{4}{5}$m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com