练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    给出问题：设是双曲线的焦点，点是双曲线上的动点，点到焦点的距离等于，求点到的距离，某同学的解答如下：双曲线的实轴长为，由即，得。试问该同学的解答是否正确？若正确，请说明依据，若不正确，请说明理由。


    根本不可能为，而只能为。


    解析:

    由定义，双曲线中，，，∴，当在同一直线上时取得“=”号，由得，在双曲线的左右支上时，，同理，，因此，根本不可能为，而只能为。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1）若椭圆的方程是：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0），它的左、右焦点依次为F1、F2，P是椭圆上异于长轴端点的任意一点．在此条件下我们可以提出这样一个问题：“设△PF1F2的过P角的外角平分线为l，自焦点F2引l的垂线，垂足为Q，试求Q点的轨迹方程？”
    对该问题某同学给出了一个正确的求解，但部分解答过程因作业本受潮模糊了，我们在
    精英家教网
    这些模糊地方划了线，请你将它补充完整．
    解：延长F2Q 交F1P的延长线于E，据题意，
    E与F2关于l对称，所以|PE|=|PF2|．
    所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=
     
    ，
    在△EF1F2中，显然OQ是平行于EF1的中位线，
    所以|OQ|=
    1
    2
    |EF1|=
     
    ，
    注意到P是椭圆上异于长轴端点的点，所以Q点的轨迹是
     
    ，
    其方程是：
     
    ．
    （2）如图2，双曲线的方程是：
    x2
    a2
    -
    y2
    b2
    =1（a，b＞0），它的左、右焦点依次为F1、F2，P是双曲线上异于实轴端点的任意一点．请你试着提出与（1）类似的问题，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•杨浦区二模）（理）设斜率为k1的直线L交椭圆C：
    x2
    2
    +y2=1    于A、B两点，点M为弦AB的中点，直线OM的斜率为k2（其中O为坐标原点，假设k1、k2都存在）．
    （1）求k1?k2的值．
    （2）把上述椭圆C一般化为
    x2
    a2
    +
    y2
    b2
    =1
    （a＞b＞0），其它条件不变，试猜想k1与k2关系（不需要证明）．请你给出在双曲线
    x2
    a2
    -
    y2
    b2
    =1    （a＞0，b＞0）中相类似的结论，并证明你的结论．
    （3）分析（2）中的探究结果，并作出进一步概括，使上述结果都是你所概括命题的特例．
    如果概括后的命题中的直线L过原点，P为概括后命题中曲线上一动点，借助直线L及动点P，请你提出一个有意义的数学问题，并予以解决．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    给出问题：设F1、F2是双曲线的焦点，点P是双曲线上的动点，点P到焦点F1的距离等于9，求点P到F2的距离，某同学的解答如下：双曲线的实轴长为8，由|PF1-PF2|=8即|9-PF2|=8，得PF2=1或PF2= 17.试问该同学的解答是否正确？若正确，请说明依据；若不正确，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2007年上海市杨浦区、静安区高考数学二模试卷（文理合卷）（解析版） 题型：解答题

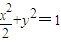    （理）设斜率为k1的直线L交椭圆C：于A、B两点，点M为弦AB的中点，直线OM的斜率为k2（其中O为坐标原点，假设k1、k2都存在）．
    （1）求k1?k2的值．
    （2）把上述椭圆C一般化为
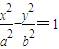    （a＞b＞0），其它条件不变，试猜想k1与k2关系（不需要证明）．请你给出在双曲线（a＞0，b＞0）中相类似的结论，并证明你的结论．
    （3）分析（2）中的探究结果，并作出进一步概括，使上述结果都是你所概括命题的特例．
    如果概括后的命题中的直线L过原点，P为概括后命题中曲线上一动点，借助直线L及动点P，请你提出一个有意义的数学问题，并予以解决．

    查看答案和解析>>

    同步练习册答案