
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据: ![]() )
)
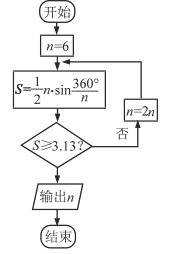
A. 12 B. 24 C. 48 D. 96
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为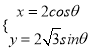 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,与直角坐标系
轴的正半轴为极轴,与直角坐标系![]() 取相同的单位长度建立极坐标系,曲线
取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)化曲线![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线![]() 与
与![]() 轴的一个交点的坐标为
轴的一个交点的坐标为![]() ,经过点
,经过点![]() 作斜率为1的直线,
作斜率为1的直线, ![]() 交曲线
交曲线![]() 于
于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,重庆成功入围国家中心城市,某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图所示茎叶图:
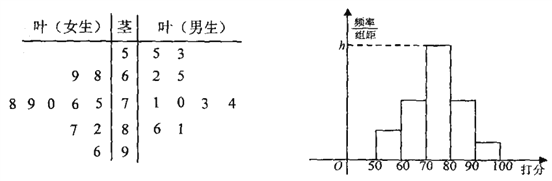
(Ⅰ)计算女生打分的平均分,并用茎叶图的数字特征评价男生、女生打分谁更分散;
(Ⅱ)如图按照打分区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 绘制的直方图中,求最高矩形的高
绘制的直方图中,求最高矩形的高![]() ;
;
(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016世界特色魅力城市![]() 强新鲜出炉,包括黄山市在内的
强新鲜出炉,包括黄山市在内的![]() 个中国城市入选. 美丽的黄山风景和人文景观迎来众多宾客. 现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了
个中国城市入选. 美丽的黄山风景和人文景观迎来众多宾客. 现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 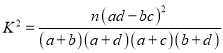
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且点
重合,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com