已知(1+x+x2)n=a+a1x+…+a2nx2n
(1)求a+a2+…+a2n的值 (2)求a1+2a2+…+2na2n的值.
【答案】
分析:(1)令已知等式中的x分别取1,-1得到两个等式,两式相加得到要求的值.
(2)先对已知等式两边分别求导数得到一个新的等式,令新等式中的x=1求出要求的系数和.
解答:解:(1)令x=1得a
+a
1+a
2+…+a
2n=3
n令x=-1得a
0-a1+a
2+…+a
2n=1
所以两式相加得a
+a
2+…+a
2n=
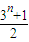
(2)对等式求导数得n(1+x+x
2)
n-1=a
1+2a
2x+3a
3x
2+…+2na
2nx
2n-1令x=1得
a
1+2a
2+…+2na
2n=3
n-1点评:求二项展开式中的系数和问题,常采用的方法是赋值法.此法的关键是通过观察给未知数赋什么值能得到要求的系数和.
