练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）求函数的单调区间和极值；

    （2）设定义在上的函数的最大值为，最小值为，且，求实数的取值范围.

    【答案】（1）极大值1，无极小值；递减区间，递增区间（2）

    【解析】

    （1）求导后，解不等式、后即可得单调区间，根据极值的概念即可求得极值；

    （2）求导得，按照、、分成3种情况，找到在上的最值，分类讨论即可得解.

    （1），定义域为

    当时，，所以在区间上为减函数，

    当时，，所以在区间上为增函数，

    所以极大值，无极小值；的递减区间，递增区间.

    （2）因为，所以

    ①当时，，在上单调递减，

    由，所以，即，得.

    ②当时，，在上单调递增，

    所以，即，得.

    ③当时，

    在，，在上单调递减，

    在，，在上单调递增.

    所以即，

    由（1）知在上单调递减，

    故，而，所以不等式无解.

    综上所述，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线的极坐标方程是,以极点为原点，以极轴为轴的正半轴，取相同的单位长度，建立平面直角坐标系，直线的参数方程为 .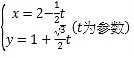

    （1）写出直线的普通方程与曲线的直角坐标方程；

    （2）设曲线经过伸缩变换得到曲线，曲线上任一点为，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”，为了响应国家政策，我市环保部门对市民进行了一次环境保护知识的网络问卷调查，每位市民仅有一次参加机会，通过随机抽样，得到参与问卷调查的50人的得分（满分：100分）数据，统计结果如表所示：

    组别

    男

    1

    2

    2

    10

    9

    6

    女

    0

    5

    5

    5

    3

    2

    若规定问卷得分不低于70分的市民称为“环境保护关注者”，则上图中表格可得列联表如下：

    非“环境保护关注者”

    是“环境保护关注者”

    合计

    男

    5

    25

    30

    女

    10

    10

    20

    合计

    15

    35

    50

    （1）请完成上述列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关？

    （2）若问卷得分不低于80分的人称为“环境保护达人”，现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答，再从这4名市民中随机抽取2人参与座谈会，求抽取的2名市民中，既有男“环境保护达人”又有女“环境保护达人”的概率.

    附表及公式：，其中.

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（），是的导数.

    （1）当时，令，为的导数.证明：在区间存在唯一的极小值点；

    （2）已知函数在上单调递减，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】推进垃圾分类处理，是落实绿色发展理念的必然选择，也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度，某社区居委会随机抽取1000名社区居民参与问卷测试，并将问卷得分绘制频率分布表如下：

    得分

    男性人数

    40

    90

    120

    130

    110

    60

    30

    女性人数

    20

    50

    80

    110

    100

    40

    20

    （1）从该社区随机抽取一名居民参与问卷测试，试估计其得分不低于60分的概率；

    （2）将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类，完成列联表，并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关？

    不太了解

    比较了解

    男性

    女性

    （3）从参与问卷测试且得分不低于80分的居民中，按照性别进行分层抽样，共抽取10人，连同名男性调查员一起组成3个环保宜传队.若从这中随机抽取3人作为队长，且男性队长人数占的期望不小于2.求的最小值.

    附：

    临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从广安市某中学校的名男生中随机抽取名测量身高，被测学生身高全部介于cm和cm之间，将测量结果按如下方式分成八组：第一组，第二组，...，第八组，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为人.

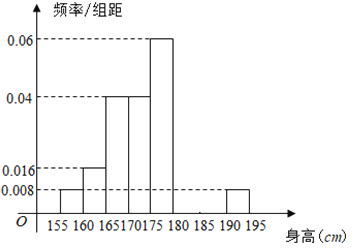
    （1）求第七组的频率；

    （2）估计该校名男生的身高的中位数。

    （3）若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生，求抽出的两名男生是同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在等腰梯形中，两腰，底边，，，是的三等分点，是的中点.分别沿，将四边形和折起，使，重合于点，得到如图2所示的几何体.在图2中，，分别为，的中点.

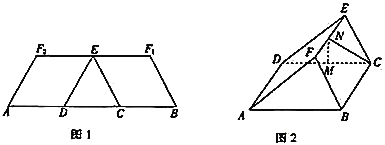
    （1）证明：平面.

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有3名医生，5名护士、2名麻醉师．

    （1）从中选派1名去参加外出学习，有多少种不同的选法？

    （2）从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组，有多少种不同的选法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在区间[0,1]上的函数y＝f(x)的图象如图所示．对满足0<x1<x2<1的任意x1，x2，给出下列结论：

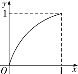
    ①f(x1)－f(x2)>x1－x2；

    ②f(x1)－f(x2)<x1－x2；

    ③x2f(x1)>x1f(x2)；

    ④．

    其中正确结论的序号是________．

    查看答案和解析>>

    同步练习册答案