
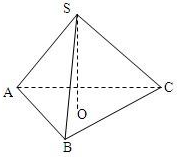
 如图,已知正三棱锥的侧棱长为2,底面周长为9.
如图,已知正三棱锥的侧棱长为2,底面周长为9.分析 (1)由正三棱锥的底面周长可知底面三角形的边长,可求出底面△ABC的面积,顶点S在底面ABC上的射影为△ABC的中心O,又在Rt△SOC中,由勾股定理求得高SO,这样可以求得三棱锥的体积;
(2)由CO>SO,在平面SOC内作SC的垂直平分线交SO的延长线于M,则M为正三棱锥的外接球的球心,连接MC,设MC=R,求出OM,再由SM=CM求得R,代入球的体积公式得答案.
解答 解:(1)如图:∵S-ABC为正三棱锥,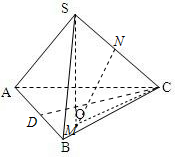
∴S在平面ABC上的射影为△ABC的中心O.
又SC=2,△ABC的周长是L△ABC=9,∴AB=3,
连接CO并延长交AB于D,则CD⊥AB,
∴CD=$\frac{\sqrt{3}}{2}$•BC=$\frac{3\sqrt{3}}{2}$,CO=$\frac{2}{3}$•CD=$\sqrt{3}$,
∴三棱锥的高SO=$\sqrt{S{C}^{2}-C{O}^{2}}$=1;
∴三棱锥的体积VS-ABC=$\frac{1}{3}$S△ABC•SO=$\frac{1}{3}×\frac{1}{2}×3×3$×sin60°×1=$\frac{3\sqrt{3}}{4}$;
(2)在平面SOC内作SC的垂直平分线交SO的延长线于M,则M为正三棱锥的外接球的球心,
连接MC,设MC=R,则OM=$\sqrt{{R}^{2}-(\sqrt{3})^{2}}=\sqrt{{R}^{2}-3}$,
由SM=CM,得$(1+\sqrt{{R}^{2}-3})^{2}={R}^{2}$,解得:R2=4,R=2.
∴这个正三棱锥的外接球的体积为$\frac{4}{3}π{R}^{3}=\frac{4}{3}π×8=\frac{32}{3}π$.
点评 本题考查了正三棱锥的体积,考查正三棱锥外接球体积的求法,考查空间想象能力和思维能力,是中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (1,+∞) | C. | (-∞,-2]∪[1,+∞) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\sqrt{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com