
| A. | (-∞,0) | B. | (1,+∞) | C. | (-∞,-2]∪[1,+∞) | D. | (-3,1) |
分析 先求导,要使函数f(x)在[t,t+2]上为单调函数,则导数符号不变化,即可求得t的取值范围.
解答 解:函数f(x)=(x2-3x+3)•ex,
那么:f′(x)=(x2-3x+3)•ex+(2x-3)ex=x(x-1)•ex
当f′(t)>0,f′(t+2)>0时,函数f(x)在[t,t+2]上为单调函数.
即:$\left\{\begin{array}{l}{{e}^{t}•t(t-1)>0}\\{{e}^{t+2}•(t+2)(t+1)>0}\end{array}\right.$
∵et>0,et+2>0
∴只需$\left\{\begin{array}{l}{t(t-1)≥0}\\{(t+2)(t+1)≥0}\end{array}\right.$,解得:t≥1或t≤-2
当f′(t)<0,f′(t+2)<0时,函数f(x)在[t,t+2]上为单调函数.
即:$\left\{\begin{array}{l}{{e}^{t}•t(t-1)<0}\\{{e}^{t+2}•(t+2)(t+1)<0}\end{array}\right.$
∵et>0,et+2>0
∴只需$\left\{\begin{array}{l}{t(t-1)≤0}\\{(t+2)(t+1)≤0}\end{array}\right.$,无解.
综上所述:t的取值范围(-∞,-2]∪[1,+∞).
故选C.
点评 本题考查了利用导数函数判断单调性的问题.属于基础题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (-∞,2)∪(2,3] | C. | (-∞,2)∪(2,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
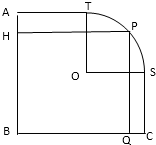 如图,图形ABCST中AB=BC=100,AB垂直于BC,O为AC的中点,AT=SC=50,弧$\widehat{TS}$以O为圆心,OT为半径,P为弧$\widehat{TS}$上任一点,过P作矩形PHBQ,求矩形PHBQ的最大面积.
如图,图形ABCST中AB=BC=100,AB垂直于BC,O为AC的中点,AT=SC=50,弧$\widehat{TS}$以O为圆心,OT为半径,P为弧$\widehat{TS}$上任一点,过P作矩形PHBQ,求矩形PHBQ的最大面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com