
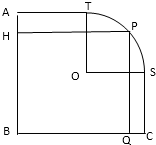
 如图,图形ABCST中AB=BC=100,AB垂直于BC,O为AC的中点,AT=SC=50,弧$\widehat{TS}$以O为圆心,OT为半径,P为弧$\widehat{TS}$上任一点,过P作矩形PHBQ,求矩形PHBQ的最大面积.
如图,图形ABCST中AB=BC=100,AB垂直于BC,O为AC的中点,AT=SC=50,弧$\widehat{TS}$以O为圆心,OT为半径,P为弧$\widehat{TS}$上任一点,过P作矩形PHBQ,求矩形PHBQ的最大面积. 分析 如图所示建立直角坐标系.设P(50cosθ,50sinθ)(θ∈$[0,\frac{π}{2}]$).可得矩形PHBQ的面积S=PH•PQ=2500(sinθcosθ+sinθ+cosθ+1).设t=sinθ+cosθ=$\sqrt{2}$$sin(θ+\frac{π}{4})$∈[1,$\sqrt{2}$],sinθcosθ=$\frac{{t}^{2}-1}{2}$,通过换元利用二次函数的单调性即可得出.
解答 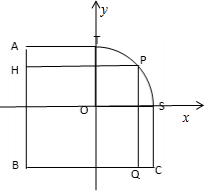 解:如图所示建立直角坐标系.
解:如图所示建立直角坐标系.
设P(50cosθ,50sinθ)(θ∈$[0,\frac{π}{2}]$).
则PH=50+50cosθ,PQ=50+50sinθ.
∴矩形PHBQ的面积S=(50+50cosθ)(50+50sinθ)
=2500(sinθcosθ+sinθ+cosθ+1),
设t=sinθ+cosθ=$\sqrt{2}$$sin(θ+\frac{π}{4})$∈[1,$\sqrt{2}$],
sinθcosθ=$\frac{{t}^{2}-1}{2}$,
则S=2500$(\frac{{t}^{2}-1}{2}+t+1)$
=1250(t+1)2,
∵S在t∈[1,$\sqrt{2}$],上单调递增.
∴当且仅当t=$\sqrt{2}$时,S取得最大值=1250(3+2$\sqrt{3}$).
点评 本题考查了圆的参数方程、三角函数基本关系式和差公式与倍角公式、三角函数的单调性,考查了换元方法、推理能力与计算能力,属于中档题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (1,+∞) | C. | (-∞,-2]∪[1,+∞) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 32 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com