
分析 (Ⅰ)已知等式两边同除anan+1化简后,根据等差数列的定义可证数列{$\frac{1}{{a}_{n}}$}为等差数列,由等差数列的通项公式求出{an}的通项公式;
(Ⅱ)由(Ⅰ)和分离常数法化简不等式,利用作差法判断数列的单调性,再求出t的取值范围.
解答 解:(Ⅰ)由题意得,2anan+1+an+1-an=0,
两边同除anan+1得,$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,
∵a1=1,∴数列{$\frac{1}{{a}_{n}}$}是以1为首项、2为公差的等差数列,
则$\frac{1}{{a}_{n}}$=1+2(n-1)=2n-1,
∴an=$\frac{1}{2n-1}$;
(Ⅱ)由(Ⅰ)得,tan+1(an-1)+1≥0为t•$\frac{1}{2n+1}$($\frac{1}{2n-1}$-1)+1≥0,
由n≥2化简得,t≤$\frac{(2n-1)(2n+1)}{2(n-1)}$,
设bn=$\frac{(2n-1)(2n+1)}{2(n-1)}$,
则bn+1-bn=$\frac{(2n+1)(2n+3)}{2n}$-$\frac{(2n-1)(2n+1)}{2(n-1)}$
=$\frac{2n+1}{2}•\frac{(2n+3)(n-1)-n(2n-1)}{n(n-1)}$=$\frac{(2n+1)(2n-3)}{2n(n-1)}$>0,
∴当n≥2时,数列{bn}是递增数列,则$\frac{(2n-1)(2n+1)}{2(n-1)}$≥$\frac{15}{2}$,
∴实数t的取值范围是(-∞,$\frac{15}{2}$].
点评 本题考查等差数列的定义、通项公式,数列的递推式的化简与应用,数列单调性的判断方法等,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x2+y2=1 | B. | x2+y2=9 | C. | x2+y2=16 | D. | x2+y2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<2 | B. | a>2或a<-1 | C. | a≥2或a≤-1 | D. | a>1或a<-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
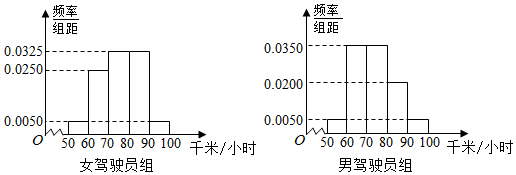
| 危险驾驶 | 非危险驾驶 | 合计 | |
| 男驾驶员 | 15 | 45 | 60 |
| 女驾驶员 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正方体ABCD-A1B1C1D1中,点M是CD的中点.
正方体ABCD-A1B1C1D1中,点M是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com