
分析 (Ⅰ)利用坐标表示出$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,可得$\overrightarrow{OP}$=(2,2),即可求|$\overrightarrow{OP}$|;
(Ⅱ)利用$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m,n∈R),即可x,y表示m-n,利用线性规划知识求出m-n的最大值.
解答 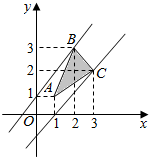 解:(Ⅰ)∵A(1,1),B(2,3),C(3,2),$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,
解:(Ⅰ)∵A(1,1),B(2,3),C(3,2),$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,
∴(1-x,1-y)+(2-x,3-y)+(3-x,2-y)=(0,0),
∴3x-6=0,3y-6=0,∴x=2,y=2,
∴$\overrightarrow{OP}$=(2,2),
∴|$\overrightarrow{OP}$|=2$\sqrt{2}$;
(Ⅱ)∵A(1,1),B(2,3),C(3,2),
∴$\overrightarrow{AB}$=(1,2),$\overrightarrow{AC}$=(2,1),
∵$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m,n∈R),
∴(x,y)=(m+2n,2m+n),
∴x=m+2n,y=2m+n,
∴m+n=y-x,
令y-x=t,由图可知,直线y=x+t过点B(2,3)时,t取得最大值1,
∴m-n的最大值为1.
点评 本题考查平面向量知识的运用,考查线性规划知识,考查 学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题. | D. | ①是假命题,②是真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:
如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
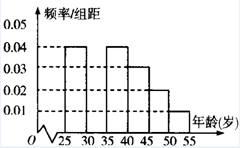 某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行
某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | P |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2) | C. | (1,$\frac{3}{2}$) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com