
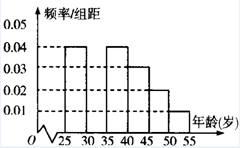
 某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行
某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | P |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
分析 (Ⅰ)先求出年龄在[25,30)岁的总人数,根据频率分布直方图,求出抽取的人数,进而求出年龄在[40,45)岁的人数,由此能求出n,a,p.
(Ⅱ)依题意,抽取年龄在[40,45)岁的有6人,抽取年龄在[45,50)岁的有3人,则X=0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)年龄在[25,30)岁的总人数为$\frac{120}{0.6}=200$,
根据频率分布直方图,抽取的人数为n=$\frac{200}{5×0.04}$=1000,
∴年龄在[40,45)岁的人数为1000×5×0.03=150,
∴a=150×0.4=60.
∵年龄在[30,35)岁的人数的频率为1-5×(0.04+0.04+0.03+0.02+0.01)=0.3,
∴年龄在[30,35)岁的人数为1000×0.3=300,
∴p=$\frac{195}{300}$=0.65.
(Ⅱ)依题意,抽取年龄在[40,45)岁的有6人,抽取年龄在[45,50)岁的有3人,
则X=0,1,2,3,
P(X=0)=$\frac{{C}_{3}^{3}}{{C}_{9}^{3}}$=$\frac{1}{84}$,
P(X=1)=$\frac{{C}_{6}^{1}{C}_{3}^{2}}{{C}_{9}^{3}}$=$\frac{18}{84}$,
P(X=2)=$\frac{{C}_{6}^{2}{C}_{3}^{1}}{{C}_{9}^{3}}$=$\frac{45}{84}$,
P(X=3)=$\frac{{C}_{6}^{3}}{{C}_{6}^{3}}$=$\frac{20}{84}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{84}$ | $\frac{18}{84}$ | $\frac{48}{84}$ | $\frac{20}{84}$ |
点评 本题考查频率分布直方图、随机变量的分布列及期望,考查数据处理能力和运算求解能力,是中档题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2 | C. | y=($\root{3}{x}$)3 | D. | y=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 90° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )
单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )| A. | 对任意点M,存在点N使截面E为三角形 | |
| B. | 对任意点M,存在点N使截面E为正方形 | |
| C. | 对任意点M和N,截面E都是梯形 | |
| D. | 对任意点N,存在点M使得截面E为矩形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com