
(本小题12分)
设 ,
, ,
,
(1)若 ,求
,求 的值;
的值;
(2)若 且
且 ,求
,求 的值;
的值;
(3)若 ,求
,求 的值.
的值.
(1)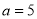 ;(2)
;(2) ;(3)
;(3)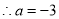 .
.
【解析】
试题分析:(1)首先由题意可求得集合B和C,然后由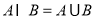 知,A=B,即集合B中的元素也是集合A中的元素,即2,3是方程
知,A=B,即集合B中的元素也是集合A中的元素,即2,3是方程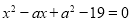 的两个根,由此即可求出
的两个根,由此即可求出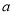 的值;
的值;
(2)由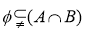 且
且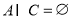 知,
知,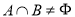 ,
,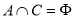 ,即
,即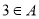 .将3代入集合A中即可求出
.将3代入集合A中即可求出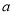 的值,并依据集合的确定性、无序性和互异性和题意条件验证其是否满足题意即可;
的值,并依据集合的确定性、无序性和互异性和题意条件验证其是否满足题意即可;
(3)由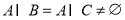 知,
知,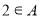 ,代入集合A中即可求出
,代入集合A中即可求出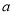 的值,并依据集合的确定性、无序性和互异性和题意条件验证其是否满足题意即可.
的值,并依据集合的确定性、无序性和互异性和题意条件验证其是否满足题意即可.
试题解析:由题可得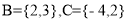 .
.
(1)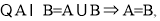 ∴2,3是方程
∴2,3是方程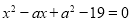 的两个根
的两个根
即
(2)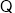
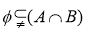 且
且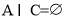 ,
,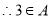 ,
,
即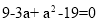
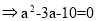
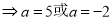
当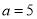 时,有
时,有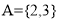 ,则
,则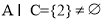 ,
,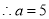 (舍去)
(舍去)
当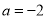 时,有
时,有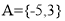 ,则
,则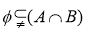 =
=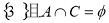 ,
,
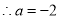 符合题意,即
符合题意,即 .
.
(3)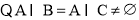 ,
,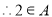 ,
,
即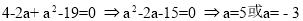 ,
,
当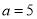 时,有
时,有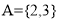 ,则
,则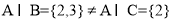 ,
,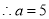 (舍去).
(舍去).
当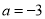 时,有
时,有 ,则
,则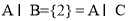 ,
,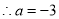 符合题意.
符合题意.
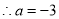 .
.
考点:集合与集合间的基本关系;集合与集合间的基本运算.


科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:选择题
已知 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 60°,若三角形有两解,则
60°,若三角形有两解,则 的取值范围是( )
的取值范围是( )
A、 B、
B、 C、
C、 D、
D、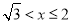
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省洛阳市高一10月月考数学试卷(解析版) 题型:选择题
已知集合 是函数
是函数 的定义域,集合
的定义域,集合 是
是 的值域,则
的值域,则 的子集的个数是( )
的子集的个数是( )
A.4 B.6 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:解答题
某企业主要生产甲、乙两种品牌的空调,由于受到空调在保修期内维修费等因素的影响,企业生产每台空调的利润与该空调首次出现故障的时间有关,甲、乙两种品牌空调的保修期均为3年,现从该厂已售出的两种品牌空调中各随机抽取50台,统计数据如下:
品牌 | 甲 | 乙 | |||||
首次出现故障时间 x年 |
|
|
|
|
|
|
|
空调数量(台) | 1 | 2 | 4 | 43 | 2 | 3 | 45 |
每台利润(千元) | 1 | 2 | 2.5 | 2.7 | 1.5 | 2.6 | 2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌空调中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的空调均能售出,记生产一台甲品牌空调的利润为X1,生产一台乙品牌空调的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌空调销量相当,但由于资金限制,只能生产其中一种品牌空调,若从经济效益的角度考虑,你认为应该生产哪种品牌的空调?说明理由。
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知某一随机变量X的分布列如下:
X | 3 | b | 8 |
P | 0.2 | 0.5 | a |
且 ,则a=__________;b=__________。
,则a=__________;b=__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com