
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析: (1)由题意知知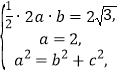 ,由此能求出椭圆
,由此能求出椭圆![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,
,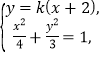 得
得![]() .,由此利用韦达定理、点到直线距离公式、直线与圆相切等知识点结合已知条件能证明当点
.,由此利用韦达定理、点到直线距离公式、直线与圆相切等知识点结合已知条件能证明当点![]() 在椭圆上运动时,以
在椭圆上运动时,以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]() ,
,
由题意知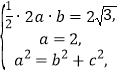 解之得
解之得![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设直线![]() 的方程为
的方程为![]() .
.
则点![]() 坐标为
坐标为![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由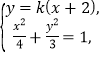 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
![]() .
.
![]() 点
点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() .
.
此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() .
.
点E到直线![]() 的距离
的距离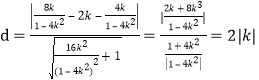 .
.
又因为![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当点![]() 在椭圆上运动时,以
在椭圆上运动时,以![]() 为直径的圆与直径
为直径的圆与直径![]() 恒相切.
恒相切.


科目:高中数学 来源: 题型:
【题目】甲、乙两人各掷一个均匀的骰子,观察朝上的面的点数,记事件A:甲得到的点数为2,B:乙得到的点数为奇数.
(1)求![]() ,
,![]() ,
,![]() ,判断事件A与B是否相互独立;
,判断事件A与B是否相互独立;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
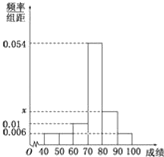
(Ⅰ)求图中![]() 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;
(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
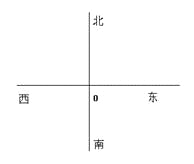
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是![]() (t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
(t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com