
【题目】设圆C满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
【答案】解法一 设圆的圆心为P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|。由题设知圆P截x轴所得劣弧所对的圆心角为90°,∴圆P截x轴所得的弦长为![]() r,故r2=2b2。 又圆P截y轴所得的的弦长为2,所以有r2=a2+1。从而得2b2-a2=1。又点P(a,b)到直线x-2y=0的距离为d=
r,故r2=2b2。 又圆P截y轴所得的的弦长为2,所以有r2=a2+1。从而得2b2-a2=1。又点P(a,b)到直线x-2y=0的距离为d=![]() ,所以5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时,上式等号成立,从而要使d取得最小值,则应有
,所以5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时,上式等号成立,从而要使d取得最小值,则应有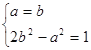 ,解此方程组得
,解此方程组得![]() 或
或![]() 。又由r2=2b2知r=
。又由r2=2b2知r=![]() 。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。------10分
。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。------10分
解法二 同解法一得d=![]() ,∴a-2b=±
,∴a-2b=±![]() d,得a2=4b2±
d,得a2=4b2±![]() bd+5d2①
bd+5d2①
将a2=2b2-1代入①式,整理得2b2±4![]() bd+5d2+1="0 " ② 把它看作b的二次方程,由于方程有实根,故判别式非负,即△=8(5d2-1)≥0,得5d2≥1。所以5d2有最小值1,从而d有最小值
bd+5d2+1="0 " ② 把它看作b的二次方程,由于方程有实根,故判别式非负,即△=8(5d2-1)≥0,得5d2≥1。所以5d2有最小值1,从而d有最小值![]() 。将其代入②式得2b2±4b+2=0,解得b=±1。将b=±1代入r2=2b2得r2=2,由r2=a2+1得a=±1。综上a=±1,b=±1,r2=2。由|a-2b|=1知a,b同号。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。--------10分
。将其代入②式得2b2±4b+2=0,解得b=±1。将b=±1代入r2=2b2得r2=2,由r2=a2+1得a=±1。综上a=±1,b=±1,r2=2。由|a-2b|=1知a,b同号。于是,所求圆的方程是(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2。--------10分
【解析】
试题本题考察的是求圆的方程,圆被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ,劣弧所对的圆心角为
,劣弧所对的圆心角为![]() ,设圆的圆心为
,设圆的圆心为![]() ,圆
,圆![]() 截
截![]() 轴所得的弦长为
轴所得的弦长为![]() ,截
,截![]() 轴所得弦长为2,可得圆心轨迹方程,圆心到直线
轴所得弦长为2,可得圆心轨迹方程,圆心到直线![]() 的距离最小,利用基本不等式,求得圆的方程.
的距离最小,利用基本不等式,求得圆的方程.
试题解析:设圆心为![]() ,半径为
,半径为![]() .
.
则![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 和
和![]() .
.
由题设知:圆截![]() 轴所得劣弧所对的圆心角为
轴所得劣弧所对的圆心角为![]() ,故圆截
,故圆截![]() 轴所得弦长为
轴所得弦长为![]() .
.
∴![]() (6分)
(6分)
又圆截![]() 轴所得弦长为2.
轴所得弦长为2.
∴![]() .又∵
.又∵![]() 到直线
到直线![]() 的距离为
的距离为
![]() (10分)∴
(10分)∴![]() .∴
.∴![]() .
.
将![]() 代入上式得:
代入上式得:![]() .
.
上述方程有实根,故
![]() ,
,
∴![]() .
.
将![]() 代入方程得
代入方程得![]() .
.
又![]() ∴
∴![]() .
.
由![]() 知
知![]() 、
、![]() 同号.
同号.
故所求圆的方程为![]() 或
或![]() .(14分)
.(14分)


科目:高中数学 来源: 题型:
【题目】小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点![]() 坐标是
坐标是![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求证直线![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() 、
、![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(9),f(27)的值
(2)解不等式f(x)+f(x﹣8)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(ω>0,|
)(ω>0,|![]() |
|![]() )在某一个周期内的图象时,列表并填入了部分数据,如下表:
)在某一个周期内的图象时,列表并填入了部分数据,如下表:
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | ﹣5 | 0 |
(1)请在答题卡上将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动![]() 个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
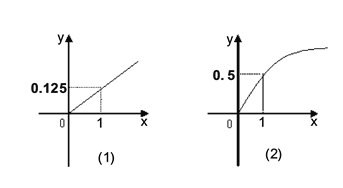
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的一年收益与投资额成正比,其关系如图(1);投资股票等风险型产品的一年收益与投资额的算术平方根成正比,其关系如图(2).(注:收益与投资额单位:万元)
(1)分别写出两种产品的一年收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使一年的投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com