
| A. | 20($\sqrt{6}$+$\sqrt{2}$) | B. | 20($\sqrt{6}$-$\sqrt{2}$) | C. | 20($\sqrt{6}$+$\sqrt{3}$) | D. | 20($\sqrt{6}$-$\sqrt{3}$) |
分析 根据题意画出相应的图形.在三角形PMN中,利用正弦定理,根据sin∠MPN与sin∠PNM的值,以及PM的长,求出MN的长,即可确定出速度.
解答 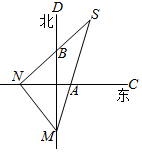 解:由题意知SM=20海里,∠SMB=15°,∠BMN=30°,∠SNC=45°,
解:由题意知SM=20海里,∠SMB=15°,∠BMN=30°,∠SNC=45°,
∴∠NMS=45°∠MNA=90°-∠BMN=60°,
∴∠SNM=105°,
∴∠MSN=30°,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=$\frac{\sqrt{6}+\sqrt{2}}{4}$
∴在△MNS中利用正弦定理可得,$\frac{MN}{sin30°}$=$\frac{20}{sin105°}$,
解得:MN=10($\sqrt{6}-\sqrt{2}$)海里,
∴货轮航行的速度v=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{2}}$=20($\sqrt{6}-\sqrt{2}$)海里/小时
故选:B.
点评 本题考查正弦定理在解三角形中的应用,解决实际问题的关键是要把实际问题转化为数学问题,再利用数学知识进行求解,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{6},\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6},\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3},\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3},\frac{π}{6}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
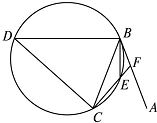 直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
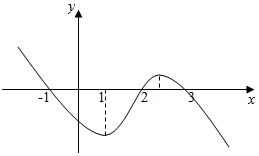 已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )
已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )| A. | (1,2)∪($\frac{5}{2}$,3)∪(-∞,-1) | B. | (-∞,-1)∪($\frac{5}{2}$,3) | C. | (-∞,-1)∪(3,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必然事件 | B. | 不可能事件 | ||
| C. | 随机事件 | D. | 以上选项均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com