
证明:把正四棱柱放置在坐标系中,则各点坐标为A(![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),B1(
,0),B1(![]() ,
,![]() ,
, ![]() ),D1(0,0,
),D1(0,0,![]() ),E(
),E(![]() ,
,![]() ,
,![]() ),F(
),F(![]() ,
,![]() ,
,![]() ).假设平面AB1C的法向量为n1=(1,λ1,μ1),则n1应垂直于
).假设平面AB1C的法向量为n1=(1,λ1,μ1),则n1应垂直于![]() 和
和![]() .而
.而![]() =(-
=(-![]() ,
,![]() ,0),
,0),![]() =(0,
=(0, ![]() ,
,![]() ),
),
∴n1·![]() =-
=-![]() +
+![]() λ1=0及n1·
λ1=0及n1·![]() =
=![]() λ1+
λ1+![]() μ1=0.
μ1=0.
∴λ1=1,μ1=-![]() .
.
∴n1=(1,1,- ![]() ).
).
再假设平面D1EF的法向量为n2=(1,λ2,μ2),则n2应垂直于![]() 、
、![]() .而
.而![]() =(
=(![]() ,
, ![]() ,-
,-![]() ),
), ![]() =(
=(![]() ,
,![]() ,-
,-![]() ),
),
∴n2·![]() =
=![]() +
+![]() λ2-
λ2-![]() μ2=0,n2·
μ2=0,n2·![]() =
=![]() +
+![]() λ2-
λ2-![]() μ2=0.
μ2=0.
∴λ2=1,μ2=![]() .
.
∴n2=(1,1, ![]() ).
).
由于n1·n2=1+1-![]() ·6=1+1-2=0,
·6=1+1-2=0,
∴n1⊥n2.因此平面D1EF⊥平面AB1C.


科目:高中数学 来源: 题型:
 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
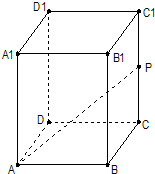 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)查看答案和解析>>
科目:高中数学 来源: 题型:
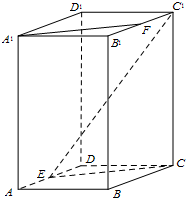 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com