
在△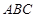 中,
中,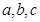 分别为三个内角
分别为三个内角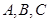 的对边,
的对边,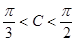 ,且
,且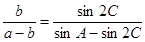 .
.
(Ⅰ) 判断△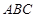 的形状;
的形状;
(Ⅱ) 若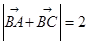 ,求
,求 的取值范围.
的取值范围.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
 (2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为
(2013•广州二模)如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P落在区 域M内的概率为| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年内江市三模文)(12分)在平面直角坐标系中,![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,平面内两点
,平面内两点![]() 同时满足一下条件:①
同时满足一下条件:①![]() ;②
;②![]() ;③
;③![]()
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与(1)中的轨迹交于
与(1)中的轨迹交于![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得以线段
,使得以线段![]() 为直径的圆过点A?若不存在,说明理由。
为直径的圆过点A?若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年内江市三模理) (12分) 在平面直角坐标系中,![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,平面内两点
,平面内两点![]() 同时满足一下条件:①
同时满足一下条件:①![]() ;②
;②![]() ;③
;③![]()
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与(1)中的轨迹交于
与(1)中的轨迹交于![]() 两点,求
两点,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳市高三高考领航考试(一)理科数学试卷(解析版) 题型:填空题
①由“若 ”类比“若
”类比“若 为三个向量,则
为三个向量,则 ”;②设圆
”;②设圆 与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则
与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则 ;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列
;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列 中,已知a1 = 0,
中,已知a1 = 0, ,则
,则 的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com