
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先考虑甲,有![]() 个位置可以选择,其他位置全排列,利用分步乘法计数原理可得出结果;
个位置可以选择,其他位置全排列,利用分步乘法计数原理可得出结果;
(2)先将甲、乙、丙三人看成一个整体,与其他四人进行排列,由此可得出排法种数;
(3)先将甲、乙二人捆绑,然后利用插空法将甲、乙这个整体与丙插入其他四人所形成的空中(包括两端),利用分步乘法计数原理可得出排法种数.
(1)甲不排头,也不排尾,则甲有![]() 个位置供选择,有
个位置供选择,有![]() 种情况;
种情况;
将其余![]() 人全排列,安排到其他位置,有
人全排列,安排到其他位置,有![]() 种排法.
种排法.
共有![]() 种排法;
种排法;
(2)采用捆绑法:先将甲、乙、丙三人看成一个整体,有![]() 种排法,将这个整体与其他四人全排列,有
种排法,将这个整体与其他四人全排列,有![]() 种排法;
种排法;
(3)先捆绑法:先将甲、乙二人看成一个整体,有![]() 种排法,再将这个整体与丙插入其他四人所形成的空中(包括两端),共有
种排法,再将这个整体与丙插入其他四人所形成的空中(包括两端),共有![]() 种.
种.
因此,共有![]() 种排法.
种排法.


科目:高中数学 来源: 题型:
【题目】已知![]() ,设实数
,设实数![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足
(i)![]() 、
、![]() 、
、![]() 且不全为0;
且不全为0;
(ii)![]() 、
、![]() 、
、![]() ;
;
(iii)若![]() ,则
,则![]() .
.
若所有形如![]() 和
和![]() 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合![]() 为“好集”.求好集
为“好集”.求好集![]() 所含元素个数的最大值.
所含元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别是
的三边长分别是![]() ,
,![]() ,
,![]() .下列说法正确的是( )
.下列说法正确的是( )
A.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为![]()
B.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为![]()
C.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为![]()
D.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
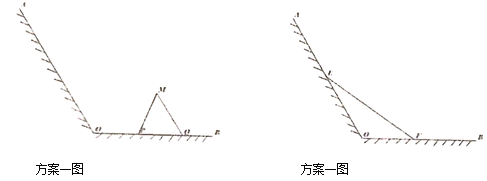
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com