
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
【答案】(1)见解析 (2)![]()
【解析】
(1)根据题意,在△AOC中,AC=a=2,AO=CO=![]() ,
,
所以AC2=AO2+CO2,所以AO⊥CO.
又AO⊥BD,BD∩CO=O,
所以AO⊥平面BCD.
(2)折叠后,BD⊥AO,BD⊥CO.所以∠AOC是二面角A-BD-C的平面角,即∠AOC=120°.在△AOC中,AO=CO=![]() ,所以AC=
,所以AC=![]() .
.
如图,过点A作CO的垂线交CO延长线于点H,
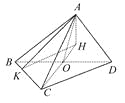
因为BD⊥CO,BD⊥AO,且CO∩AO=O,所以BD⊥平面AOC.因为AH平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.所以AH⊥BC.过点A作AK⊥BC,垂足为K,连接HK,因为BC⊥AH,AK∩AH=A,所以BC⊥平面AHK.因为HK平面AHK,所以BC⊥HK.所以∠AKH为二面角A-BC-D的平面角.
在△AOH中,得AH=![]() ,OH=
,OH=![]() ,所以CH=CO+OH=
,所以CH=CO+OH=![]() +
+![]() =
=![]() .
.
在Rt△CHK中,HK=![]() =,
=,
在Rt△AHK中,tan∠AKH=![]() =
=![]() =
=![]() .
.
所以二面角A-BC-D的正切值为![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
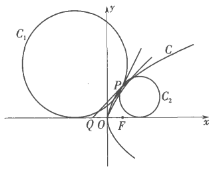
【题目】如图,在平面直角坐标系xOy中,F为x轴正半轴上的一个动点.以F为焦点、O为顶点作抛物线C.设P为第一象限内抛物线C上的一点,Q为x轴负半轴上一点,使得PQ为抛物线C的切线,且![]() .圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
.圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:
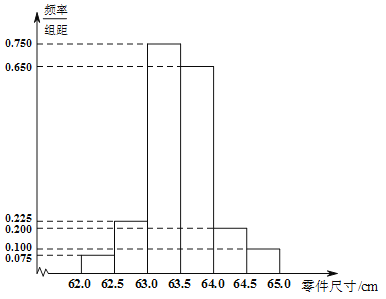
注:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(Ⅰ) 从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅱ) 从产品中随机抽取![]() 件,全是合格品的概率不小于
件,全是合格品的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ) 为了提高产品合格率,现提出![]() 两种不同的改进方案进行试验.若按
两种不同的改进方案进行试验.若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ;若按
;若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设函数![]() 的定义域为
的定义域为![]() ,且有极值点.
,且有极值点.
(ⅰ) 试判断当![]() 时,
时, ![]() 是否满足题目的条件,并说明理由;
是否满足题目的条件,并说明理由;
(ⅱ) 设函数![]() 的极小值点为
的极小值点为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵![]() 中,
中,![]() .
.

(1)求证:四棱锥![]() 为阳马;并判断四面体
为阳马;并判断四面体![]() 是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
(2)若![]() ,当阳马
,当阳马![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com