
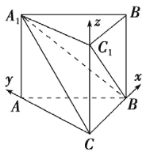
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵![]() 中,
中,![]() .
.

(1)求证:四棱锥![]() 为阳马;并判断四面体
为阳马;并判断四面体![]() 是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
(2)若![]() ,当阳马
,当阳马![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;是,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由堑堵![]() 的性质得:四边形
的性质得:四边形![]() 是矩形,推导出
是矩形,推导出![]() ,
,![]() ,从而BC⊥平面
,从而BC⊥平面![]() ,由此能证明四棱锥
,由此能证明四棱锥![]() 为阳马,四面体
为阳马,四面体![]() 是否为鳖臑;
是否为鳖臑;
(2)阳马B﹣A1ACC1的体积:阳马![]() 的体积:
的体积:![]()
![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出当阳马
轴,建立空间直角坐标系,利用向量法能求出当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的余弦值.
的余弦值.
证明:(1)由堑堵![]() 的性质得:四边形
的性质得:四边形![]() 是矩形,
是矩形,![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,![]() 四棱锥
四棱锥![]() 为阳马,
为阳马,
四面体![]() 为鳖臑,四个面的直角分别是
为鳖臑,四个面的直角分别是![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]() ,由(1)知阳马
,由(1)知阳马![]() 的体积:
的体积:
![]()
![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则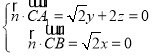 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则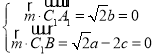 ,取
,取![]() ,得
,得![]() ,
,
设当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的平面角为
的平面角为![]() ,则
,则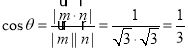 ,
,
当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,纵、横坐标都是整数的点称为整点。请设计一种方法将所有的整点染色,每一个整点染成白色、红色或黑色中的一种颜色,使得
(1)每一种颜色的点出现在无穷多条平行于横轴的直线上;
(2)对于任意白点![]() 、红点
、红点![]() 及黑点
及黑点![]() ,总可以找到一个红点
,总可以找到一个红点![]() ,使
,使![]() 为一平行四边形。证明你设计的方法符合上述要求。
为一平行四边形。证明你设计的方法符合上述要求。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,DA=DC=2,![]() ,E是C1D1的中点,F是CE的中点.
,E是C1D1的中点,F是CE的中点.
(1)求证:EA∥平面BDF;
(2)求证:平面BDF⊥平面BCE;
(3)求二面角D﹣EB﹣C的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铜陵市出租车已于今年6月1日起调整运价,现行计价标准是:路程在2.5km以内(含2.5km)按起步价7元收取,超过2.5km后的路程按1.9元km收取,但超过8km后的路程需加收50%的返空费(即单价为![]() 元).
元).
(1)将某乘客搭乘一次出租车的费用![]() (单位:元)表示为行程x(
(单位:元)表示为行程x(![]() ,单位:km)的分段函数;
,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆出租车行驶8km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,B1E⊥平面ABC,△AB1C是等边三角形,AB=2A1B1,AC=2BC,∠ACB=90°.
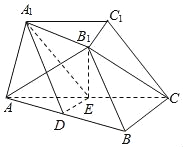
(1)证明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com