
【题目】铜陵市出租车已于今年6月1日起调整运价,现行计价标准是:路程在2.5km以内(含2.5km)按起步价7元收取,超过2.5km后的路程按1.9元km收取,但超过8km后的路程需加收50%的返空费(即单价为![]() 元).
元).
(1)将某乘客搭乘一次出租车的费用![]() (单位:元)表示为行程x(
(单位:元)表示为行程x(![]() ,单位:km)的分段函数;
,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆出租车行驶8km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?请说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设函数![]() 的定义域为
的定义域为![]() ,且有极值点.
,且有极值点.
(ⅰ) 试判断当![]() 时,
时, ![]() 是否满足题目的条件,并说明理由;
是否满足题目的条件,并说明理由;
(ⅱ) 设函数![]() 的极小值点为
的极小值点为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵![]() 中,
中,![]() .
.

(1)求证:四棱锥![]() 为阳马;并判断四面体
为阳马;并判断四面体![]() 是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
(2)若![]() ,当阳马
,当阳马![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家提出的“大众创业,万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业。经过市场调查,生产某小型电子产品需投入年固定成本为5万元,每年生产![]() 万件,需另投入流动成本为
万件,需另投入流动成本为![]() 万元,且
万元,且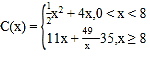 ,每件产品售价为10元。经市场分析,生产的产品当年能全部售完。
,每件产品售价为10元。经市场分析,生产的产品当年能全部售完。
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,且与
,且与![]() 轴有唯一的交点
轴有唯一的交点![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,记此函数的最小值为
,记此函数的最小值为![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
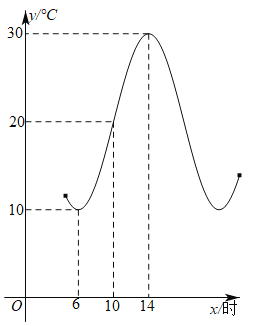
A.该函数的周期是![]()
B.该函数图象的一条对称轴是直线![]()
C.该函数的解析式是![]()
D.该市这一天中午![]() 时天气的温度大约是
时天气的温度大约是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个判断正确的是______(写出所有正确判断的序号.)
①函数![]() 是奇函数,但不是偶函数;
是奇函数,但不是偶函数;
②函数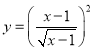 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
③已知函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ,则
,则![]() 的值为
的值为![]() ;
;
④设函数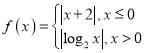 ,若关于
,若关于![]() 的方程
的方程![]() 有四个不同的解
有四个不同的解![]() ,且
,且![]() ,则
,则![]() 的值为
的值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(1)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(2)若圆![]() 的半径为1,过点
的半径为1,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(3)有一动圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com