练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点，点，圆

    (1)求过点的圆的切线方程；

    (2)求过点的圆的切线方程．

    【答案】（1）；（2）或

    【解析】

    由圆的方程可得圆心坐标和半径；

    （1）验证可知在圆上，利用两点连线斜率公式可得；根据垂直关系可求得切线斜率，由直线点斜式可求得切线方程，整理可得结果；

    （2）验证可知在圆外；当过的直线斜率不存在时，易知是圆切线；当过的直线斜率存在时，假设直线方程，利用圆心到直线距离等于半径可构造方程求得切线斜率，代入整理可得结果.

    由题意得：圆心，半径

    （1） 在圆上

    切线的斜率

    过点的圆的切线方程为，即

    （2） 在圆外部

    若过点的直线斜率不存在，直线方程为，是圆的切线；

    若过点的切线斜率存在，可设切线方程为：，即

    圆心到切线的斜率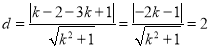，解得：

    切线方程为，即

    综上所述：切线方程为或

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥，底面，底面为等腰梯形，，，，，点E为边上的点，.

    （1）求证：平面；

    （2）若，求点E到平面的距离 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是平行四边形，且，，平面平面.

    （1）求证：；

    （2）若底面是边长为2的菱形，四棱锥的体积为，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，纵、横坐标都是整数的点称为整点。请设计一种方法将所有的整点染色，每一个整点染成白色、红色或黑色中的一种颜色，使得

    （1）每一种颜色的点出现在无穷多条平行于横轴的直线上；

    （2）对于任意白点、红点及黑点，总可以找到一个红点，使为一平行四边形。证明你设计的方法符合上述要求。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,设点为椭圆的右焦点，圆过且斜率为的直线交圆于两点，交椭圆于点两点，已知当时，

    （1）求椭圆的方程.

    （2）当时，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义域为的奇函数，当.

    （Ⅰ）求出函数在上的解析式；

    （Ⅱ）在答题卷上画出函数的图象，并根据图象写出的单调区间；

    （Ⅲ）若关于的方程有三个不同的解，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，长方体ABCD﹣A1B1C1D1中，DA＝DC＝2，，E是C1D1的中点，F是CE的中点．

    （1）求证：EA∥平面BDF；

    （2）求证：平面BDF⊥平面BCE；

    （3）求二面角D﹣EB﹣C的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】铜陵市出租车已于今年6月1日起调整运价，现行计价标准是：路程在2.5km以内（含2.5km）按起步价7元收取，超过2.5km后的路程按1.9元km收取，但超过8km后的路程需加收50%的返空费（即单价为元）.

    （1）将某乘客搭乘一次出租车的费用（单位：元）表示为行程x（，单位：km）的分段函数；

    （2）某乘客的行程为16km，他准备先乘一辆出租车行驶8km后，再换乘另一辆出租车完成余下行程，请问：他这样做是否比只乘一辆出租车完成全部行程更省钱?请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，判断是否为的极值点，并说明理由；

    （2）记.若函数存在极大值，证明：.

    查看答案和解析>>

    同步练习册答案