
【题目】(1)已知数列![]() ,其中
,其中![]() ,且数列
,且数列![]() 为等比数列,求常数p;
为等比数列,求常数p;
(2)设![]() 、
、![]() 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,![]() ,证明:数列
,证明:数列![]() 不是等比数列.
不是等比数列.
【答案】(1)p=2或p=3;(2)证明见解析.
【解析】
(1)第一问中,利用给定的等比数列,结合定义得到p的值;(2)根据设![]() 、
、![]() 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,![]() ,那么可验证前几项是否是等比数列来判定结论.
,那么可验证前几项是否是等比数列来判定结论.
(1)因为{cn+1-pcn}是等比数列,
故有:(cn+1-pcn)2=(cn+2-pcn+1)(cn-pcn-1),将cn=2n+3n代入上式,得:
[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)],
即[(2-p)2n+(3-p)3n]2
=[(2-p)2n+1+(3-p)3n+1][(2-p)2n-1+(3-p)3n-1],
整理得![]() (2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2)证明:设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn.
为证{cn}不是等比数列只需证c22≠c1·c3.
事实上,c22=(a1p+b1q)2=a12p2+b12q2+2a1b1pq,
c1·c3=(a1+b1)(a1p2+b1q2)=a12p2+b12q2+a1b1(p2+q2),
由于p≠q,p2+q2>2pq,又a1、b1不为零,
因此c22≠c1·c3,
故{cn}不是等比数列.
本试题主要是考查了等比数列的概念的运用.


科目:高中数学 来源: 题型:
【题目】某城市现有人口总数为![]() 万人,如果年自然增长率为
万人,如果年自然增长率为![]() ,试解答下列问题:
,试解答下列问题:
(1)写出该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式;
的函数关系式;
(2)用程序流程图表示计算![]() 年以后该城市人口总数的算法;
年以后该城市人口总数的算法;
(3)用程序流程图表示如下算法:计算大约多少年以后该城市人口将达到![]() 万人.
万人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(注意:在试题卷上作答无效)
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止;
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
求依方案甲所需化验次数不少于依方案乙所需化验次数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为“三角形”数列,对于“三角形”数列
为“三角形”数列,对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”,
的“保三角形函数”,![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() 是数列
是数列![]() 的“保三角形函数”,求
的“保三角形函数”,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的首项为2010,
的首项为2010,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3)根据“保三角形函数的定义,对函数![]() ,和数列1,
,和数列1,![]() 提出一个正确的命题,并说明理由.
提出一个正确的命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
, ![]() 为
为![]() 上一点,
上一点,![]() 为菱形
为菱形![]() 对角线的交点.
对角线的交点.
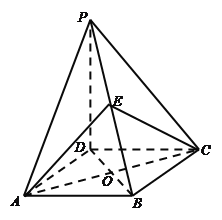
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,四棱锥
,四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

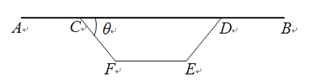
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com