
【题目】某城市现有人口总数为![]() 万人,如果年自然增长率为
万人,如果年自然增长率为![]() ,试解答下列问题:
,试解答下列问题:
(1)写出该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式;
的函数关系式;
(2)用程序流程图表示计算![]() 年以后该城市人口总数的算法;
年以后该城市人口总数的算法;
(3)用程序流程图表示如下算法:计算大约多少年以后该城市人口将达到![]() 万人.
万人.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)利用指数函数的定义可得出该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式;
的函数关系式;
(2)根据(1)中求得的函数解析式,利用循环结构框图可表示计算![]() 年以后该城市人口总数的算法;
年以后该城市人口总数的算法;
(3)根据(1)中所求的函数解析式,即求满足![]() 成立的最小正整数
成立的最小正整数![]() ,在判断框图就可以设定判断条件为
,在判断框图就可以设定判断条件为![]() ,当条件满足时继续循环;当条件不满足时跳出循环体.由此可利用程序框图来表示算法:计算大约多少年以后该城市人口将达到
,当条件满足时继续循环;当条件不满足时跳出循环体.由此可利用程序框图来表示算法:计算大约多少年以后该城市人口将达到![]() 万人.
万人.
(1)一年后,该城市的人口数为![]() ;
;
二年后,该城市的人口数为![]() ;
;
![]() ;
;
![]() 年后,该城市的人口数为
年后,该城市的人口数为![]() .
.
因此,该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式为
的函数关系式为![]() ;
;
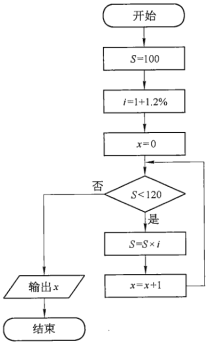
(2)程序框图如下图所示:

(3)程序框图如下图所示:


科目:高中数学 来源: 题型:
【题目】
已知函数![]() 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”;若函数
和性质”;若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 积性质”.
积性质”.
(1) 判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数![]() 对任何
对任何![]() ,满足“
,满足“![]() 积性质”.求
积性质”.求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家具公司制作木质的书桌和椅子,需要木工和漆工两道工序,已知木工平均四个小时做一把椅子,八个小时做一张书桌,该公司每星期木工最多有8000个工作时;漆工平均两小时漆一把椅子、一小时漆一张书桌,该公司每星期漆工最多有1300个工作时,又已知制作一把椅子和一张书桌的利润分别是15元和20元,试根据以上条件,问怎样安排生产能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).至少3人同时上网的概率为________;至少________人同时上网的概率小于0.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com