
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
【答案】(1)当t≤0时,f(x)在(0,+∞)上单调递增;当t>0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减;(2)证明见解析.
,+∞)上单调递减;(2)证明见解析.
【解析】
(1)求导后分![]() 和
和![]() 两种情况讨论极值点的大小关系以及导函数的正负,进而求得原函数的单调区间即可.
两种情况讨论极值点的大小关系以及导函数的正负,进而求得原函数的单调区间即可.
(2)代入![]() ,根据f(x)=m﹣ax,可得
,根据f(x)=m﹣ax,可得![]() 的两根分别为
的两根分别为![]() ,再消去
,再消去![]() 化简得到
化简得到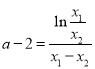 ,再代入所证的
,再代入所证的![]() ,换元令
,换元令![]() ,进而求导分析导数的正负以及原函数的单调性即可.
,进而求导分析导数的正负以及原函数的单调性即可.
(1)f(x)的定义域为(0,+∞),f′(x)![]() ,
,
当t≤0时,f′(x)>0恒成立,f(x)在(0,+∞)上单调递增,
当t>0时,令f′(x)>0,得0<x![]() ,令f′(x)<0,得x
,令f′(x)<0,得x![]() .
.
∴f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
综上所述,当t≤0时,f(x)在(0,+∞)上单调递增;
当t>0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
(2)证明:由f(x)=m﹣ax,得lnx+(a﹣2)x+2﹣m=0.
令g(x)=lnx+(a﹣2)x+2,则g(x1)=g(x2)=m.
即lnx1+(a﹣2)x1=lnx2+(a﹣2)x2,
∴a﹣2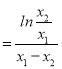 .
.
不妨设0<x1<x2,要证![]() ,
,
只需证![]() 2(2﹣a)
2(2﹣a)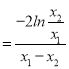 ,即证
,即证![]() .
.
令![]() (c>1),g(c)=2lnc﹣c
(c>1),g(c)=2lnc﹣c![]() ,
,
∵g′(c)![]() 0.
0.
∴g(c)在(1,+∞)上单调递减,则g(c)<g(1)=0.
故![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某工厂的一台某型号机器有2种工作状态:正常状态和故障状态.若机器处于故障状态,则停机检修.为了检查机器工作状态是否正常,工厂随机统计了该机器以往正常工作状态下生产的1000个产品的质量指标值,得出如图1所示频率分布直方图.由统计结果可以认为,这种产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为这1000个产品的质量指标值的平均数
近似为这1000个产品的质量指标值的平均数![]() ,
,![]() 近似为这1000个产品的质量指标值的方差
近似为这1000个产品的质量指标值的方差![]() (同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在
(同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在![]() 之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
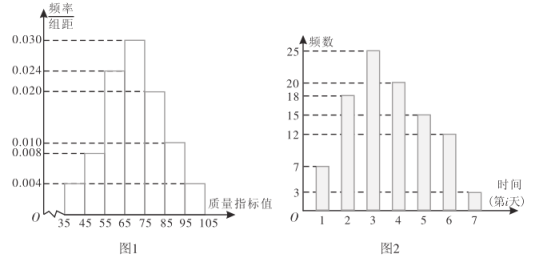
(1)下面是检验员在一天内从该机器生产的产品中随机抽取10件测得的质量指标值:
29 45 55 63 67 73 78 87 93 113
请判断该机器是否出现故障?
(2)若机器出现故障,有2种检修方案可供选择:
方案一:加急检修,检修公司会在当天排除故障,费用为700元;
方案二:常规检修,检修公司会在七天内的任意一天来排除故障,费用为200元.
现需决策在机器出现故障时,该工厂选择何种方案进行检修,为此搜集检修公司对该型号机器近100单常规检修在第i(![]() ,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
附:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市现有人口总数为![]() 万人,如果年自然增长率为
万人,如果年自然增长率为![]() ,试解答下列问题:
,试解答下列问题:
(1)写出该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式;
的函数关系式;
(2)用程序流程图表示计算![]() 年以后该城市人口总数的算法;
年以后该城市人口总数的算法;
(3)用程序流程图表示如下算法:计算大约多少年以后该城市人口将达到![]() 万人.
万人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,边
,边![]() 上一点
上一点![]() ,这里
,这里![]() 异于
异于![]() .由
.由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,再由
是垂足,再由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,又由
是垂足,又由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足.同样的操作连续进行,得到点
是垂足.同样的操作连续进行,得到点![]() ,
,![]() ,
,![]() .设
.设![]() ,如图所示.
,如图所示.

(1)求![]() 的值;
的值;
(2)某同学对上述已知条件的研究发现如下结论:![]() ,问该同学这个结论是否正确并说明理由;
,问该同学这个结论是否正确并说明理由;
(3)用![]() 和
和![]() 表示
表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
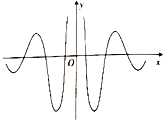
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
, ![]() 为
为![]() 上一点,
上一点,![]() 为菱形
为菱形![]() 对角线的交点.
对角线的交点.
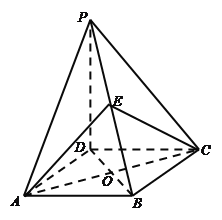
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,四棱锥
,四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com