
| A. | [0,30°] | B. | [0,45°] | C. | [0,60°] | D. | [0,90°] |
分析 根据直线和圆的位置关系即可得到结论.
解答 解:若直线斜率不存在,此时x=-$\sqrt{3}$与圆没有交点,
则直线斜率k一定存在,设为k,
则过P的直线方程为y+1=k(x+$\sqrt{3}$),
即kx-y+$\sqrt{3}$k-1=0,
若过点P(-$\sqrt{3}$,-1)的直线l与圆x2+y2=1有公共点,
则圆心到直线的距离d≤1,
即$\frac{|\sqrt{3}k-1|}{\sqrt{1+{k}^{2}}}$≤1,即|$\sqrt{3}$k-1|≤$\sqrt{1+{k}^{2}}$,
平方得k2-$\sqrt{3}$k≤0,
解得0≤k≤$\sqrt{3}$,
即0≤tanα≤$\sqrt{3}$,
解得0°≤α≤60°,
故选:C.
点评 本题主要考查直线和圆的位置关系的应用以及直线倾斜角的求解,根据条件转化为圆心到直线的距离和半径之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
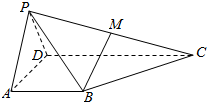 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 买1张肯定不中奖 | B. | 买100张一定恰有一张能中奖 | ||
| C. | 买100张一定能中奖 | D. | 买100张未必能中奖 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
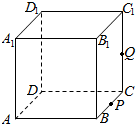 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的中点,则四面体A1PQD的正视图、侧视图和俯视图的面积之和为( )| A. | $\frac{5}{4}$ | B. | 2 | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a>2b | B. | ${(\frac{1}{3})^a}>{(\frac{1}{3})^b}$ | C. | a2>b2 | D. | lg(a-b)>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com