
【题目】如图,在三棱柱![]() 中,底面
中,底面![]() 是边长为4的等边三角形,
是边长为4的等边三角形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
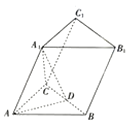
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() 是等边三角形,求二面角
是等边三角形,求二面角![]() 的正弦值.
的正弦值.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)现给出三个条件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
试从中选出两个可以确定![]() 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求![]() 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为点
的左、右焦点分别为点![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,长轴长为
,长轴长为![]() ,椭圆上任意一点
,椭圆上任意一点![]() (不与
(不与![]() 重合)与
重合)与![]() 连线的斜率乘积均为
连线的斜率乘积均为![]() .
.
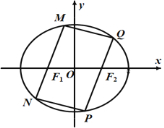
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试问:四边形
,试问:四边形![]() 可否为菱形?并请说明理由.
可否为菱形?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知二次函数![]() (
(![]() 、
、![]() 、
、![]() 均为实常数,
均为实常数,![]() )的最小值是0,函数
)的最小值是0,函数![]() 的零点是
的零点是![]() 和
和![]() ,函数
,函数![]() 满足
满足![]() ,其中
,其中![]() ,为常数.
,为常数.
(1)已知实数![]() 、
、![]() 满足、
满足、![]() ,且
,且![]() ,试比较
,试比较![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中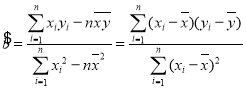 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
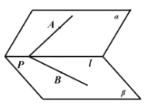
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某冰糖橙,甜橙的一种,云南著名特产,以味甜皮薄著称。该橙按照等级可分为四类:珍品、特级、优级和一级(每箱有5kg),某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱,利用橙子的等级分类标准得到的数据如下表:
等级 | 珍品 | 特级 | 优级 | 一级 |
箱数 | 40 | 30 | 10 | 20 |
(1)若将频率改为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好抽到2箱是一级品的概率:
(2)利用样本估计总体,庄园老板提出两种购销方案供采购商参考:
方案一:不分等级卖出,价格为27元/kg;
方案二:分等级卖出,分等级的橙子价格如下:
等级 | 珍品 | 特级 | 优级 | 一级 |
售价(元/kg) | 36 | 30 | 24 | 18 |
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的是珍品等级,求x的分布列及数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com