
【题目】已知椭圆![]() 的左、右焦点分别为点
的左、右焦点分别为点![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,长轴长为
,长轴长为![]() ,椭圆上任意一点
,椭圆上任意一点![]() (不与
(不与![]() 重合)与
重合)与![]() 连线的斜率乘积均为
连线的斜率乘积均为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
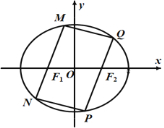
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试问:四边形
,试问:四边形![]() 可否为菱形?并请说明理由.
可否为菱形?并请说明理由.
【答案】(1)![]() ;(2)不是.
;(2)不是.
【解析】
(1)由长轴长为![]() 可得
可得![]() ,然后结合
,然后结合![]() 求得
求得![]() 的值,从而得到椭圆方程;
的值,从而得到椭圆方程;
(2)根据![]() 以及椭圆的对称性可得
以及椭圆的对称性可得![]() 为平行四边形,其对角线交点为原点
为平行四边形,其对角线交点为原点![]() ,设出直线
,设出直线![]() 的方程为
的方程为![]() 与椭圆方程联立,由韦达定理可得
与椭圆方程联立,由韦达定理可得![]() ,
,![]() ,故要使四边形
,故要使四边形![]() 为菱形,则
为菱形,则![]() ,利用向量表示出
,利用向量表示出![]() ,整理可得
,整理可得![]() ,解方程则可得到答案。
,解方程则可得到答案。
(1)由题意,![]() ,则
,则![]() ,
,![]() 。设
。设![]() ,则点
,则点![]() 与点
与点![]() 连线的斜率为
连线的斜率为![]() ,点
,点![]() 与点
与点![]() 连线的斜率为
连线的斜率为![]() ,故
,故![]() ,又因为点
,又因为点![]() 在椭圆
在椭圆![]() 上,故有
上,故有![]() ,联立解得
,联立解得![]() ,
,
则椭圆![]() 的方程为
的方程为![]() .
.
(2)由于点![]() 关于原点对称且
关于原点对称且![]() ,故
,故![]() 关于原点对称,又椭圆关于原点对称,所以四边形
关于原点对称,又椭圆关于原点对称,所以四边形![]() 为平行四边形;由(1),知
为平行四边形;由(1),知![]() ,易知直线
,易知直线![]() 不能平行于
不能平行于![]() 轴.所以令直线
轴.所以令直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() .联立方程
.联立方程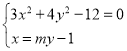 ,得
,得![]() ,所以
,所以![]() ,
,![]() .若
.若![]() 是菱形,则
是菱形,则![]() ,即
,即![]() ,于是有
,于是有![]() ,整理得到
,整理得到![]() ,即
,即![]() ,上述关于
,上述关于![]() 的方程显然没有实数解,故四边形
的方程显然没有实数解,故四边形![]() 不可能是菱形.
不可能是菱形.


科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
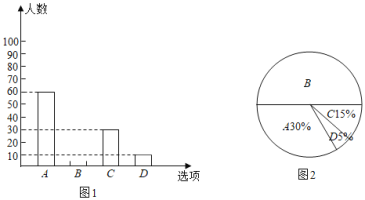
(1)本次一共调查了多少名学生.
(2)在图(1)中将![]() 对应的部分补充完整.
对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,离心率等于
的中心在坐标原点,离心率等于![]() ,该椭圆的一个长轴端点恰好是抛物线
,该椭圆的一个长轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 的两个交点记为
的两个交点记为![]() 、
、![]() ,其中点
,其中点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当
两侧的动点.当![]() 、
、![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值?若是,求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
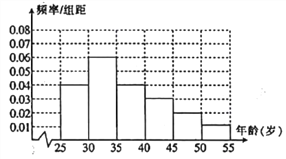
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数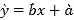 ,回归直线方程
,回归直线方程![]() ,
,
其中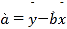 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因事故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
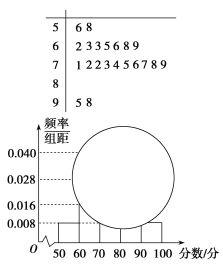
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com