
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设函数 ,若
,若![]() ,且
,且![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若
,若![]() ,且
,且![]() 在
在![]() 上存在零点,求
上存在零点,求![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求导后,根据导函数的符号即可确定单调区间;(2)分别在![]() 和
和![]() 两种情况下,判断恒成立的条件;当
两种情况下,判断恒成立的条件;当![]() 时,利用二次函数的性质,结合
时,利用二次函数的性质,结合![]() 可构造不等式求得
可构造不等式求得![]() 的范围;当
的范围;当![]() 时,利用分离变量法得到
时,利用分离变量法得到![]() 恒成立,进而通过求解右侧函数最小值得到
恒成立,进而通过求解右侧函数最小值得到![]() 的范围;两个范围取交集即为最终结果;(3)将函数在
的范围;两个范围取交集即为最终结果;(3)将函数在![]() 上存在零点转化为
上存在零点转化为![]() 在
在![]() 上有解的问题;通过讨论
上有解的问题;通过讨论![]() 的正负可分离变量变为
的正负可分离变量变为![]() ,利用导数求解不等式右侧函数的最大值得到结果.
,利用导数求解不等式右侧函数的最大值得到结果.
(1)当![]() 时,
时,![]()
![]()
令![]() 得:
得:![]()
![]() 函数
函数![]() 的定义域为
的定义域为![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]()
(2)由![]() 得:
得: .
.
当![]() 时,
时,![]() 恒成立
恒成立
当![]() ,即
,即![]() 时,
时,![]() 恒成立;
恒成立;
当![]() ,即
,即![]() 时,
时,![]()
解得:![]()
综上所述:![]()
当![]() 时,由
时,由![]() 恒成立得:
恒成立得:![]() 恒成立
恒成立
设![]() ,则
,则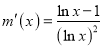 .
.
令![]() 得:
得:![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]()
![]()
综上所述:![]() 的取值范围为:
的取值范围为:![]()
(3)![]()
![]() 在
在![]() 上存在零点
上存在零点 ![]() 在
在![]() 上有解
上有解
即![]() 在
在![]() 上有解
上有解
又![]() ,即
,即![]()
![]() 在
在![]() 上有解
上有解
设![]() ,则
,则![]()
令![]() 得:
得:![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,
![]() ,即
,即![]()
![]() .
.
设![]() ,则
,则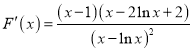
同理可证:![]()
![]()
则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]() ,故
,故![]()
![]() 的取值范围为:
的取值范围为:![]()


科目:高中数学 来源: 题型:
【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线L:![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数)
为参数)
![]() 求直线L和曲线C的普通方程;
求直线L和曲线C的普通方程;
![]() 在曲线C上求一点Q,使得Q到直线L的距离最小,并求出这个最小值
在曲线C上求一点Q,使得Q到直线L的距离最小,并求出这个最小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过
经过![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点在圆
的中点在圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)直线![]() 不过曲线
不过曲线![]() 的右焦点
的右焦点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() 与圆
与圆![]() 相切,切点在第一象限,
相切,切点在第一象限, ![]() 的周长是否为定值?并说明理由.
的周长是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为点
的左、右焦点分别为点![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,长轴长为
,长轴长为![]() ,椭圆上任意一点
,椭圆上任意一点![]() (不与
(不与![]() 重合)与
重合)与![]() 连线的斜率乘积均为
连线的斜率乘积均为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
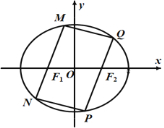
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试问:四边形
,试问:四边形![]() 可否为菱形?并请说明理由.
可否为菱形?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市10万名男生的身高服从正态分布![]() .现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
.现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
分组 | [160,166) | [166,172) | [172,178) | [178,184) | [184,190] |
人数 | 3 | 10 | 24 | 10 | 3 |
这50个数据的平均数和方差分别比10万个数据的平均数和方差多1和6.68,且这50个数据的方差为![]() .(同组中的身高数据用该组区间的中点值作代表):
.(同组中的身高数据用该组区间的中点值作代表):
(1)求![]() ,
,![]() ;
;
(2)给出正态分布的数据:![]() ,
,![]() .
.
(i)若从这10万名学生中随机抽取1名,求该学生身高在(169,179)的概率;
(ii)若从这10万名学生中随机抽取1万名,记![]() 为这1万名学生中身高在(169,184)的人数,求
为这1万名学生中身高在(169,184)的人数,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中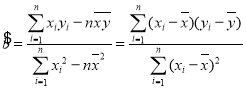 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com