
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上是单调递增函数,求实数
上是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,对任意
,对任意![]() ,不等式
,不等式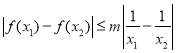 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟).
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 34 | 51 | 59 | 66 | 65 | 25 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 40 | 160 | |
合计 |
(2)通过计算判断,是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关?
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因事故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
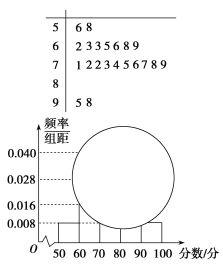
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过点
的焦点重合,过点![]() 与
与![]() 的长轴垂直的直线交
的长轴垂直的直线交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与
与![]() 相切,且与
相切,且与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019年”是一个重要的时间节点——中华人民共和国成立70周年,和全面建成小康社会的 关键之年.70年披荆斩棘,70年砥砺奋进,70年风雨兼程,70年沧桑巨变,勤劳勇敢的中国 人用自己的双手创造了一项项辉煌的成绩,取得了举世瞩目的成就.趁此良机,李明在天猫网店销售“新中国成立70周年纪念册”,每本纪念册进价4元,物流费、管理费共为![]() 元/本,预计当每本纪念册的售价为
元/本,预计当每本纪念册的售价为![]() 元(
元(![]() 时,月销售量为
时,月销售量为![]() 千本.
千本.
(I)求月利润![]() (千元)与每本纪念册的售价X的函数关系式,并注明定义域:
(千元)与每本纪念册的售价X的函数关系式,并注明定义域:
(II)当![]() 为何值时,月利润
为何值时,月利润![]() 最大?并求出最大月利润.
最大?并求出最大月利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com