
【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
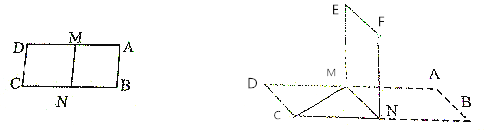
(1)求证:直线CM⊥面DFN;
(2)求点C到平面FDM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到了如表的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为患心肺疾病与性别有关?说明你的理由.
参考格式:![]() ,其中
,其中![]() .
.
下面的临界值仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求三角形的面积的公式,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即 ,其中a、b、c分别为
,其中a、b、c分别为![]() 内角A、B、C的对边.若
内角A、B、C的对边.若![]() ,
,![]() ,则
,则![]() 面积S的最大值为
面积S的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的![]() 赛,
赛,![]() 两队各由4名选手组成,每局两队各派一名选手
两队各由4名选手组成,每局两队各派一名选手![]() ,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛
,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛![]() 队选手获胜的概率均为
队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时
,且各局比赛结果相互独立,比赛结束时![]() 队的得分高于
队的得分高于![]() 队的得分的概率为( )
队的得分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]() 点
点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,
两点,![]() 为
为![]() 上任意一点,直线
上任意一点,直线![]() 交
交![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com