练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆经过为坐标原点，线段的中点在圆上.

    （1）求的方程；

    （2）直线不过曲线的右焦点，与交于两点，且与圆相切，切点在第一象限， 的周长是否为定值？并说明理由.

    【答案】（1）（2）

    【解析】试题分析：（1）由题意，可得： ，从而得到的方程；

    （2）依题意可设直线，由直线与圆相切，且切点的第一象限，可得，将直线与椭圆方程联立可得，利用韦达定理表示，同时表示，同理，从而易得周长为定值.

    试题解析：

    （1）由题意得，

    由题意得， 的中点在圆上，

    所以，得，

    所以椭圆方程为.

    （2）依题意可设直线，

    因为直线与圆相切，且切点的第一象限，

    所以，且有，

    设，将直线与椭圆方程联立

    可得， ， ，且

    ，

    因为，故，

    另一方面

    ，

    化简得，同理，可得，

    由此可得的周长，

    故的周长为定值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在如图所示的五面体中， ， ， ，四边形为正方形，平面平面．

    （1）证明：在线段上存在一点，使得平面；

    （2）求的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】共享单车因绿色、环保、健康的出行方式，在国内得到迅速推广.最近，某机构在某地区随机采访了10名男士和10名女士，结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”，其他人表示“较少或不选择骑共享单车出行”.

    （1）从这些男士和女士中各抽取一人，求至少有一人“经常骑共享单车出行”的概率；

    （2）从这些男士中抽取一人，女士中抽取两人，记这三人中“经常骑共享单车出行”的人数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正四棱锥的各条棱长都相等，且点分别是的中点.

    （1）求证: ；

    （2）在上是否存在点，使平面平面，若存在，求出的值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

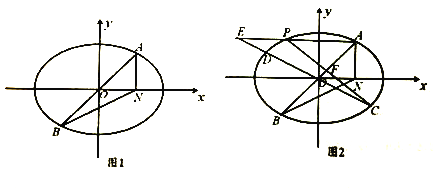
    【题目】在平面直角坐标系中，已知直线与椭圆交于点， （在轴上方），且.设点在轴上的射影为，三角形的面积为2（如图1）.

    （1）求椭圆的方程；

    （2）设平行于的直线与椭圆相交，其弦的中点为.

    ①求证：直线的斜率为定值；

    ②设直线与椭圆相交于两点， （在轴上方），点为椭圆上异于， ， ， 一点，直线交于点， 交于点，如图2，求证： 为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1， 在直角梯形中， ， ， ， 为线段的中点. 将沿折起，使平面 平面，得到几何体，如图2所示.

    （1）求证: 平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（为参数），在以为极点， 轴的正半轴为极轴的极坐标系中，曲线是圆心为，半径为1的圆.

    （1）求曲线， 的直角坐标方程；

    （2）设为曲线上的点， 为曲线上的点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数.

    （1）若函数在上为减函数，求实数的取值范围；

    （2）令，已知函数，若对任意，总存在 ，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆与直线都经过点.直线与平行，且与椭圆交于两点，直线与轴分别交于两点.

    （1）求椭圆的方程；

    （2）证明： 为等腰三角形.

    查看答案和解析>>

    同步练习册答案